题目内容
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,
M为AP的中点.
(Ⅰ)求证:DM∥平面PCB;
(Ⅱ)求直线AD与PB所成角;
(Ⅲ)求三棱锥P-MBD的体积.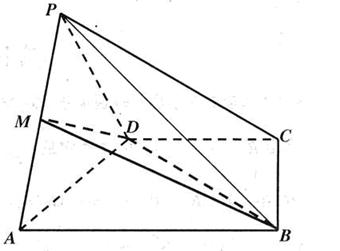
M为AP的中点.
(Ⅰ)求证:DM∥平面PCB;
(Ⅱ)求直线AD与PB所成角;
(Ⅲ)求三棱锥P-MBD的体积.

(Ⅰ)证明见解析(Ⅱ)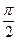 (Ⅲ)
(Ⅲ)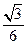
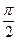 (Ⅲ)
(Ⅲ)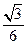
(I)取PB的中点F,联结MF、CF,∵M、F分别为PA、PB的中点.
∴MF∥AB,且MF=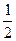 AB.
AB.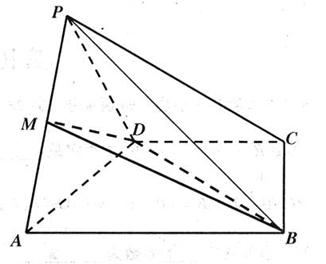
∵四边形ABCD是直角梯形,AB∥CD且AB=2CD,
∴MF∥CD且MF=CD.
∴四边形CDFM是平行四边形.
∴DM∥CF.
∵CF平面PCB,
∴DM∥平面PCB. 4分
(Ⅱ)取AD的中点G,连结PG、GB、BD.
∵PA=PD, ∴PG⊥AD.
∵AB=AD,且∠DAB=60°,
∴△ABD是正三角形,BG⊥AD.
∴AD⊥平面PGB.
∴AD⊥PB. 8分
(Ⅲ)VP-MBD=VB-PMD 10分
VB-PMD =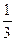 ×
×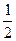 ×
×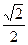 ×
×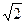 ×
×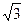 =
=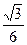 14分
14分
∴MF∥AB,且MF=
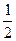 AB.
AB.
∵四边形ABCD是直角梯形,AB∥CD且AB=2CD,
∴MF∥CD且MF=CD.
∴四边形CDFM是平行四边形.
∴DM∥CF.
∵CF平面PCB,
∴DM∥平面PCB. 4分
(Ⅱ)取AD的中点G,连结PG、GB、BD.
∵PA=PD, ∴PG⊥AD.
∵AB=AD,且∠DAB=60°,
∴△ABD是正三角形,BG⊥AD.
∴AD⊥平面PGB.
∴AD⊥PB. 8分
(Ⅲ)VP-MBD=VB-PMD 10分
VB-PMD =
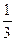 ×
×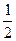 ×
×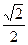 ×
×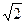 ×
×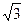 =
=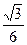 14分
14分
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD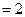 , AD=1, EF=
, AD=1, EF=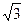 .
.
 平面FCB;
平面FCB;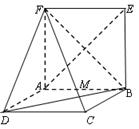
 为菱形,
为菱形,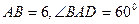 ,两个正三棱锥
,两个正三棱锥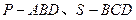 (底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点
(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点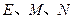 分别在
分别在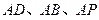 上,且
上,且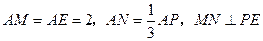 .
.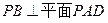 ;
;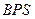 与底面
与底面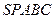 的体积.
的体积. 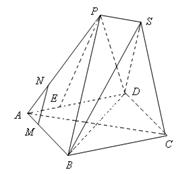
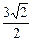
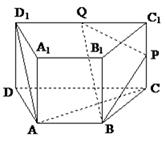
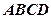 中,
中,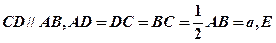 是
是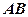 的中点,将
的中点,将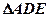 沿
沿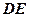 折起,使点
折起,使点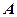 到点
到点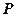 的位置,使二面角
的位置,使二面角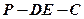 的大小为
的大小为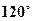
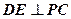 ;
;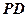 与平面
与平面 所成角的正弦值
所成角的正弦值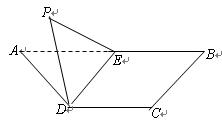
 ⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).
⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).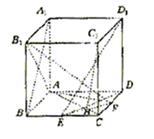
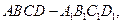
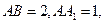
 直线
直线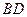 与平面
与平面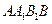 所成的角为
所成的角为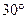 ,
,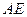 垂直
垂直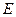 ,
,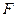 为
为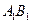 的中点.
的中点.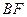 所成的角;
所成的角;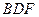 与平面
与平面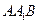 所成的二面角;
所成的二面角;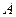 到平面
到平面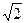 ,PB⊥PD.
,PB⊥PD.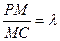 ,问
,问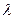 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.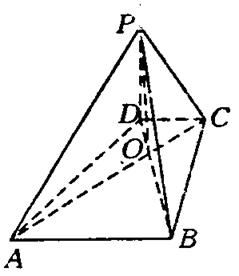
 V的水。
V的水。