题目内容
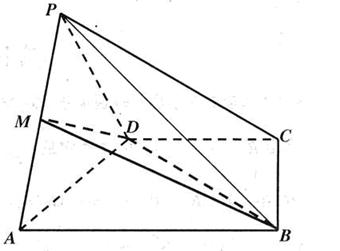
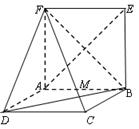
矩形ABCD与矩形ABEF的公共边为AB,且平面ABCD 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD , AD=1, EF=
, AD=1, EF=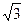 .
.

(Ⅰ)证明:AE 平面FCB;
平面FCB;
(Ⅱ)求异面直线BD与AE所成角的余弦值
(Ⅲ)若M是棱AB的中点,在线段FD上是否存在一点N,使得MN∥平面FCB?
证明你的结论.
 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD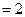 , AD=1, EF=
, AD=1, EF=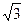 .
.
(Ⅰ)证明:AE
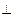 平面FCB;
平面FCB;(Ⅱ)求异面直线BD与AE所成角的余弦值
(Ⅲ)若M是棱AB的中点,在线段FD上是否存在一点N,使得MN∥平面FCB?
证明你的结论.

(Ⅰ)见解析
(Ⅱ)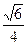
(Ⅲ)见解析
(Ⅱ)
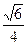
(Ⅲ)见解析
(1)
 平面ABCD
平面ABCD 平面ABEF,
平面ABEF,且四边形ABCD与ABEF是矩形,
 AD
AD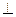 平面ABEF,
平面ABEF,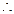 AD
AD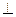 AE,
AE, 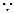 BC∥AD
BC∥AD 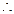 BC
BC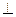 AE
AE又FD=2,AD=1,所以AF=EF=
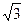 ,
,所以四边形ABEF为正方形.
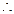 AE
AE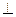 FB,
FB,又BF
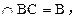 BF
BF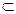 平面BCF,BC
平面BCF,BC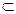 平面BCF
平面BCF所以AE
 平面BCF……………………………………………4分
平面BCF……………………………………………4分(2)设BF
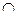 AE=O,取FD的中点为H,连接OH,在
AE=O,取FD的中点为H,连接OH,在 OH//BD,
OH//BD,
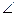 HOF即为异面直线BD与AE所成的角(或补角),
HOF即为异面直线BD与AE所成的角(或补角),在
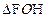 中,OH=1,FH=1,FO=
中,OH=1,FH=1,FO=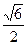 ,
,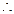 cos
cos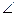 HOF=
HOF=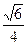
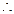 异面直线BD与AE所成的角的余弦值为
异面直线BD与AE所成的角的余弦值为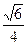 ………………………….8分
………………………….8分(3)当N为FD的中点时, MN∥平面FCB
证明:取CD的中点G,连结NG,MG,MN,
则NG//FC,MG//BC,
又NG
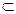 平面NGM,MG
平面NGM,MG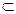 平面NGM且NG
平面NGM且NG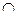 MG=G
MG=G所以平面NGM//平面FBC,
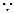 MN
MN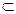 平面NGM
平面NGM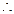 MN//平面FBC……………………………………………………………12分
MN//平面FBC……………………………………………………………12分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

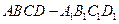 中,
中, 分别是
分别是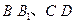 的中点.
的中点. 
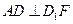 ; (2)求
; (2)求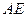 与
与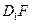 所成的角;
所成的角;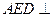 面
面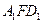 ;(4)
;(4)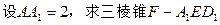 的体积
的体积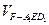
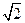 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点。
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点。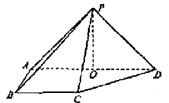
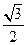 ?若存在,求出
?若存在,求出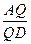 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。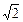 ,EF=EC=1,
,EF=EC=1, 
 中
中
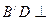 平面
平面 ;
;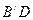 与平面
与平面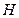 是
是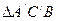 的重心(三角形三条中线的交点)
的重心(三角形三条中线的交点)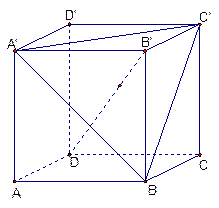
 平面BCD;
平面BCD;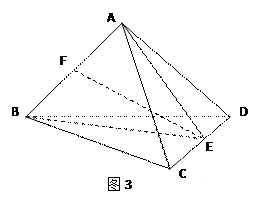
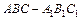 中,
中,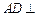 平面
平面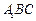 ,其垂足
,其垂足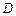 落在直线
落在直线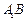 上.
上.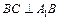 ;
;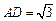 ,
,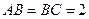 ,
,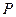 为
为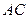 的中点,求三棱锥
的中点,求三棱锥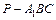 的体积.
的体积.