题目内容
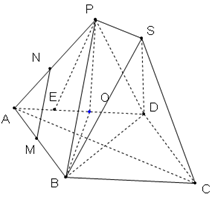
已知四边形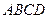 为菱形,
为菱形,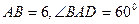 ,两个正三棱锥
,两个正三棱锥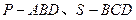 (底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点
(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点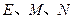 分别在
分别在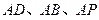 上,且
上,且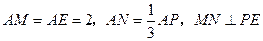 .
.
(Ⅰ)求证: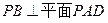 ;
;
(Ⅱ)求平面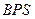 与底面
与底面 所成锐二面角的平面角的正切值;
所成锐二面角的平面角的正切值;
(Ⅲ)求多面体 的体积.
的体积.
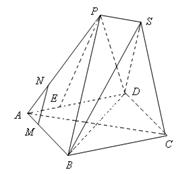
 为菱形,
为菱形,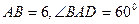 ,两个正三棱锥
,两个正三棱锥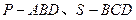 (底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点
(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点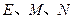 分别在
分别在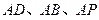 上,且
上,且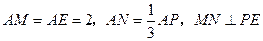 .
.(Ⅰ)求证:
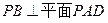 ;
;(Ⅱ)求平面
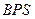 与底面
与底面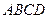 所成锐二面角的平面角的正切值;
所成锐二面角的平面角的正切值;(Ⅲ)求多面体
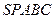 的体积.
的体积. 
(Ⅰ) 见解析(Ⅱ) 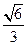 (Ⅲ)
(Ⅲ)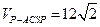
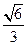 (Ⅲ)
(Ⅲ)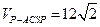
(Ⅰ)取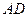 中点
中点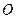 ,连
,连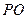 、
、 ,则
,则
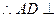 面
面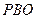 ,
,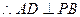
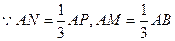
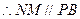
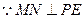
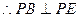
又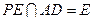
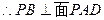 ……………3分
……………3分
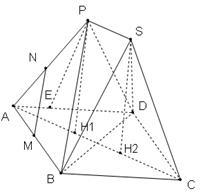
(Ⅱ)设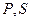 在底面的射影分别为
在底面的射影分别为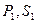 ,则
,则
由所给的三棱锥均为正三棱锥且两三棱锥全等,
故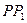 ∥
∥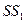 ,且
,且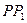 =
=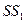 ,∴四边形
,∴四边形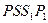 为平行四边形,
为平行四边形,
∴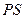 ∥
∥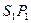 ,又
,又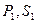 分别为△
分别为△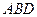 ,△
,△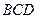 的中心,
的中心,
∴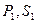 在菱形的对角线
在菱形的对角线 上,
上,
∴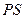 ∥
∥ ,即
,即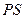 ∥平面
∥平面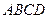 …………………………………5分
…………………………………5分
设平面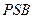 与平面
与平面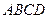 的交线为
的交线为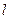 ,取
,取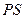 中点
中点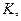 连结
连结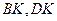 ,
,
由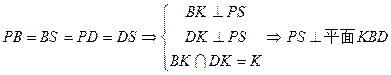
∴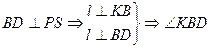 为平面
为平面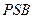 与平面
与平面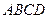 所成二面角的平面角
所成二面角的平面角
…………………………7分
在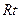 △
△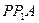 中,
中, 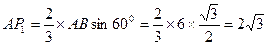 ,
,
∴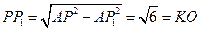 ,
,
∴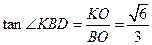 ……………………………9分
……………………………9分
(Ⅲ设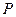 、
、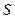 在
在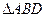 和
和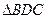 上的射影为
上的射影为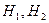 ,则
,则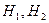 均在直线
均在直线 上,且
上,且 为平行四边形,
为平行四边形,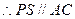 。
。
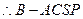 为四棱锥 设
为四棱锥 设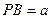 ,则
,则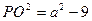 ,又
,又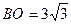 ,由(1)知
,由(1)知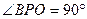
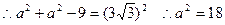 即
即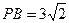
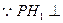 面
面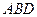 ,
,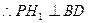 ,又
,又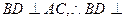 面
面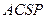 。
。
设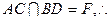 四棱锥
四棱锥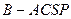 的高为
的高为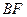 ,且
,且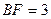
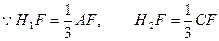
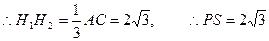 在
在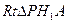 中,
中,
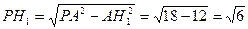
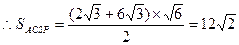
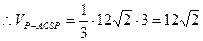 ……………13分
……………13分
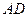 中点
中点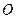 ,连
,连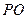 、
、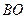 ,则
,则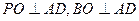


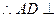 面
面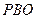 ,
,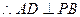
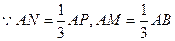
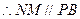
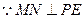
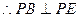
又
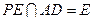
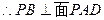 ……………3分
……………3分(Ⅱ)设
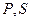 在底面的射影分别为
在底面的射影分别为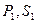 ,则
,则由所给的三棱锥均为正三棱锥且两三棱锥全等,
故
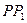 ∥
∥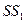 ,且
,且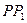 =
=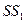 ,∴四边形
,∴四边形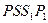 为平行四边形,
为平行四边形,∴
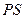 ∥
∥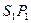 ,又
,又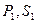 分别为△
分别为△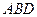 ,△
,△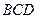 的中心,
的中心,∴
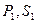 在菱形的对角线
在菱形的对角线 上,
上,∴
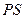 ∥
∥ ,即
,即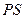 ∥平面
∥平面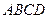 …………………………………5分
…………………………………5分设平面
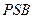 与平面
与平面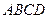 的交线为
的交线为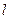 ,取
,取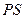 中点
中点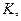 连结
连结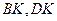 ,
,由
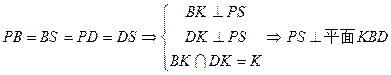
∴
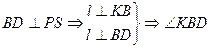 为平面
为平面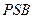 与平面
与平面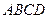 所成二面角的平面角
所成二面角的平面角…………………………7分
在
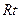 △
△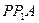 中,
中, 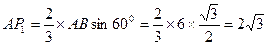 ,
,∴
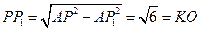 ,
,∴
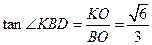 ……………………………9分
……………………………9分(Ⅲ设
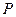 、
、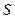 在
在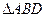 和
和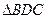 上的射影为
上的射影为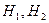 ,则
,则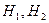 均在直线
均在直线 上,且
上,且 为平行四边形,
为平行四边形,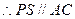 。
。
|
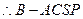 为四棱锥 设
为四棱锥 设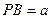 ,则
,则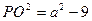 ,又
,又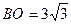 ,由(1)知
,由(1)知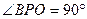
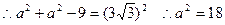 即
即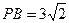
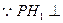 面
面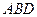 ,
,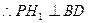 ,又
,又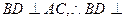 面
面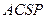 。
。设
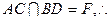 四棱锥
四棱锥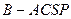 的高为
的高为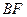 ,且
,且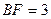
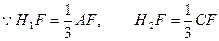
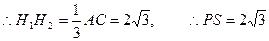 在
在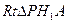 中,
中,
|
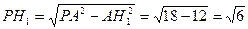
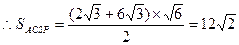
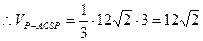 ……………13分
……………13分
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
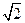 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点。
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点。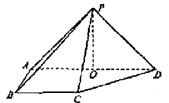
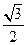 ?若存在,求出
?若存在,求出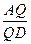 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 平面BCD;
平面BCD;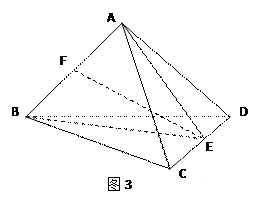
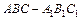 中,
中,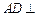 平面
平面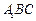 ,其垂足
,其垂足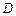 落在直线
落在直线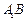 上.
上.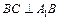 ;
;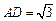 ,
,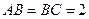 ,
,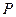 为
为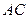 的中点,求三棱锥
的中点,求三棱锥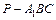 的体积.
的体积.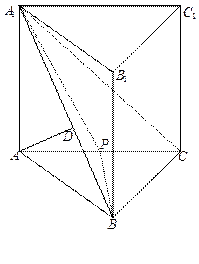
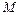 是
是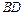 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角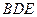 ?若存在,确定点N的位置;
?若存在,确定点N的位置;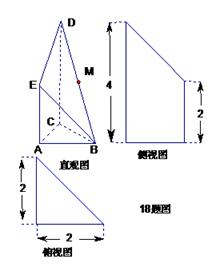
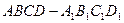 的底面ABCD是菱形,且
的底面ABCD是菱形,且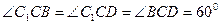 ,(1)证明:
,(1)证明: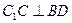 ;
;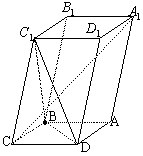
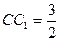 ,记面
,记面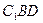 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;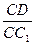 的值为多少时,能使
的值为多少时,能使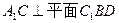 ?请给出证明.
?请给出证明. 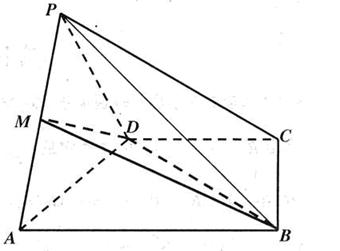
 ⊥平面
⊥平面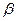 ,那么
,那么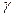 ,平面
,平面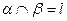 ,那么
,那么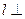 平面
平面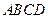 的顶点
的顶点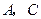 在椭圆
在椭圆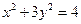 上,对角线
上,对角线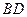 所在直线的斜率为1.
所在直线的斜率为1.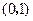 时,求直线
时,求直线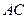 的方程;
的方程; 时,求菱形
时,求菱形