题目内容
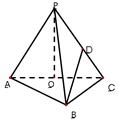
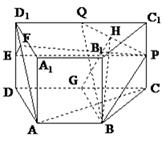
如图,直四棱柱ABCD-A1B1C1D1的底面是
梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点。点P到直线
AD1的距离为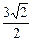
⑴求证:AC∥平面BPQ
⑵求二面角B-PQ-D的大小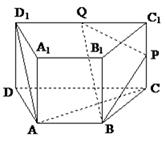
梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点。点P到直线
AD1的距离为
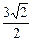
⑴求证:AC∥平面BPQ
⑵求二面角B-PQ-D的大小

(Ⅰ)证明见解析(Ⅱ)arctan

⑴连接CD1∵P、Q分别是CC1、C1D1的
中点。∴CD1∥PQ 故CD1∥平面BPQ
 又D1Q=AB=1,D1Q∥AB,
又D1Q=AB=1,D1Q∥AB,
得平行四边形ABQD1,故AD1∥平面BPQ
∴平面ACD1∥平面BPQ
∴AC∥平面BPQ (4分)
⑵设DD1中点为E,连EF,则PE∥CD
∵CD⊥AD,CD⊥DD1 ∴CD⊥平面ADD1
∴PE⊥平面ADD1
过E作EF⊥AD1于F,连PF。则PF⊥AD1,PF为点P到直线AD1的距离
PF=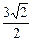 ,PE="2 " ∴EF=
,PE="2 " ∴EF=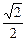 又D1E=
又D1E=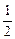 ,D1D=1,∴AD="1 "
,D1D=1,∴AD="1 "
取CD中点G,连BG,由AB∥DG,AB=DG得GB∥AD。∵AD⊥DC,AD⊥DD1∴AD⊥平面DCC1D1,则BG⊥平面DCC1D1
过G作GH⊥PQ于H,连BH,则BH⊥PQ,故∠BHG是二面角B-PQ-D的平面角。
由△GHQ∽△QC1P得GH=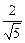 ,又BG=1,得tan∠BHG=
,又BG=1,得tan∠BHG=
∴二面角B-PQ-D大小为arctan
中点。∴CD1∥PQ 故CD1∥平面BPQ
 又D1Q=AB=1,D1Q∥AB,
又D1Q=AB=1,D1Q∥AB,得平行四边形ABQD1,故AD1∥平面BPQ
∴平面ACD1∥平面BPQ
∴AC∥平面BPQ (4分)
⑵设DD1中点为E,连EF,则PE∥CD
∵CD⊥AD,CD⊥DD1 ∴CD⊥平面ADD1
∴PE⊥平面ADD1
过E作EF⊥AD1于F,连PF。则PF⊥AD1,PF为点P到直线AD1的距离
PF=
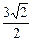 ,PE="2 " ∴EF=
,PE="2 " ∴EF=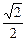 又D1E=
又D1E=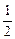 ,D1D=1,∴AD="1 "
,D1D=1,∴AD="1 " 取CD中点G,连BG,由AB∥DG,AB=DG得GB∥AD。∵AD⊥DC,AD⊥DD1∴AD⊥平面DCC1D1,则BG⊥平面DCC1D1
过G作GH⊥PQ于H,连BH,则BH⊥PQ,故∠BHG是二面角B-PQ-D的平面角。
由△GHQ∽△QC1P得GH=
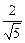 ,又BG=1,得tan∠BHG=
,又BG=1,得tan∠BHG=
∴二面角B-PQ-D大小为arctan


练习册系列答案
相关题目
 中
中
 平面
平面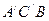 ;
;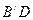 与平面
与平面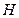 是
是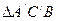 的重心(三角形三条中线的交点)
的重心(三角形三条中线的交点)
 是
是 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角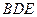 ?若存在,确定点N的位置;
?若存在,确定点N的位置;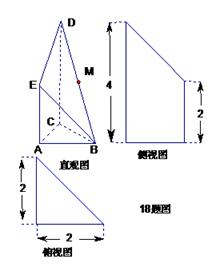
 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0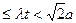 。
。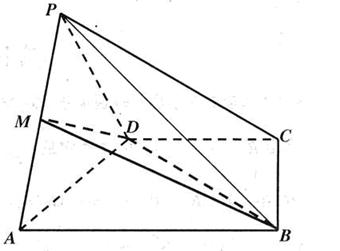
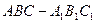 中,
中,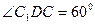 .
.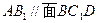 (5分)
(5分)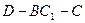 的大小。(7分)
的大小。(7分)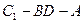 平面角的大小。(7分)
平面角的大小。(7分)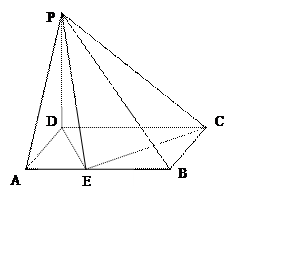 已知PD=
已知PD=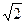 ,CD=2,AE=
,CD=2,AE=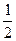 ,
,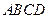 中,底面
中,底面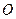 是正方形
是正方形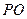
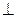 底面
底面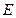 是
是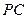 的中点.
的中点.
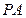 ∥平面
∥平面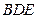 ;
;