题目内容
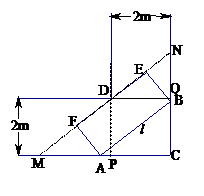
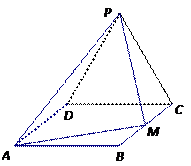
如图,已知四棱锥P—ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=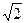 ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P—AB—C的大小;
(Ⅲ)设点M在棱PC上,且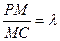 ,问
,问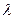 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.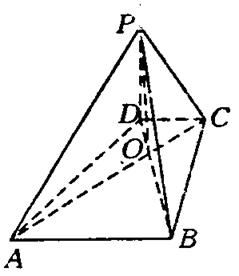
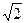 ,PB⊥PD.
,PB⊥PD.(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P—AB—C的大小;
(Ⅲ)设点M在棱PC上,且
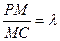 ,问
,问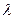 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
(Ⅰ)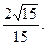 (Ⅱ)45°(Ⅲ)
(Ⅱ)45°(Ⅲ)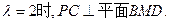
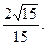 (Ⅱ)45°(Ⅲ)
(Ⅱ)45°(Ⅲ)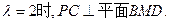
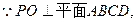

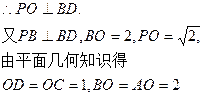
以O为原点,OA,OB,OP分别为x,y,z轴建立如图所示的空间直角坐标系,则各点坐标为O(0,0,0),A(2,0,0),B(0,2,0),C(-1,0,0),D(0,-1,0),P(0,0,
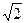 ).
).(1)
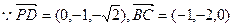 ,
,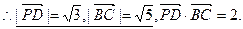
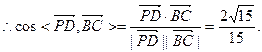
故直线PD与BC所成的角的余弦值为
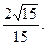
(2)设平面PAB的一个法向量为
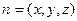 ,
,由于
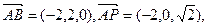
由
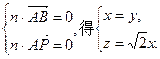
取
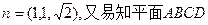 的一个法向量
的一个法向量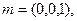
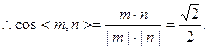
又二面角P—AB—C不锐角.
∴所求二面角P—AB—C的大小为45°
(3)设
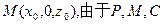 三点共线,
三点共线,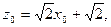
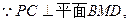 (1)
(1)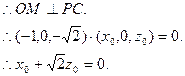 (2)
(2)由(1)(2)知

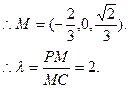
故
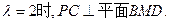

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 平面BCD;
平面BCD;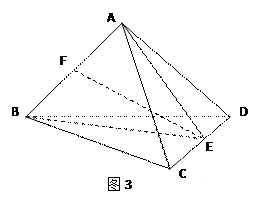
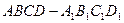 的底面ABCD是菱形,且
的底面ABCD是菱形,且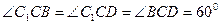 ,(1)证明:
,(1)证明: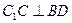 ;
;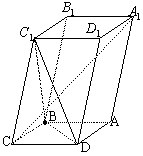
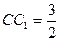 ,记面
,记面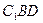 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;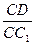 的值为多少时,能使
的值为多少时,能使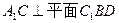 ?请给出证明.
?请给出证明. 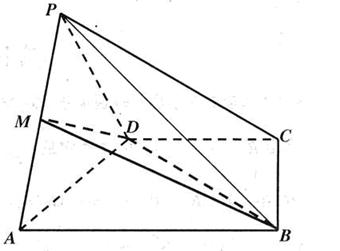
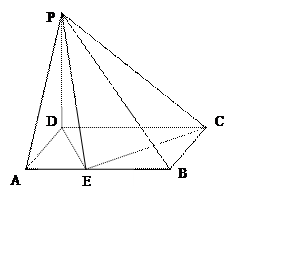 已知PD=
已知PD=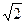 ,CD=2,AE=
,CD=2,AE=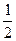 ,
,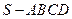 的底面是正方形,
的底面是正方形,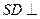 平面
平面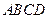 .
.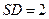 ,
,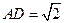 ,
,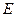 是
是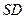 上的点.
上的点.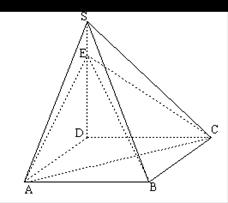
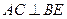 ;
;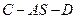 的余弦值.
的余弦值.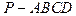 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且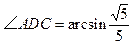 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。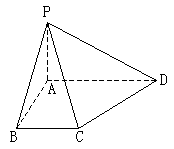
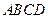 的顶点
的顶点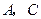 在椭圆
在椭圆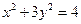 上,对角线
上,对角线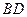 所在直线的斜率为1.
所在直线的斜率为1.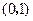 时,求直线
时,求直线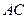 的方程;
的方程; 时,求菱形
时,求菱形