题目内容
17.设F1,F2分别是椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点,过点M且斜率为k的直线l与椭圆C交于A、B两点,O是坐标原点.(1)若M(0,$\sqrt{5}$),椭圆与x轴正半轴、y轴正半轴交点分别为P、Q,问:是否存在常数k,使向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与$\overrightarrow{pQ}$共线;
(2)若M为椭圆C的右焦点,且$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}B}$,求k的值;
(3)若M为椭圆C的左顶点,Q为线段AB的垂直平分线与y轴的交点,且$\overrightarrow{QA}•\overrightarrow{QB}$=4,求点Q的坐标.
分析 (1)设A(x1,y1),B(x2,y2),则$\overrightarrow{OA}$+$\overrightarrow{OB}$=(x1+x2,y1+y2),由直线方程和椭圆方程联立,消去y,可得x的方程,运用韦达定理和判别式,再由向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与$\overrightarrow{pQ}$=(-2,1)共线等价于x1+x2=-2(y1+y2),由此能求出不存在这样的常数k满足条件;
(2)设A(x1,y1),B(x2,y2),由直线y=k(x-$\sqrt{3}$),代入椭圆方程x2+4y2=4,运用韦达定理,再由向量共线的坐标表示,解方程可得k;
(3)求出椭圆的左顶点为A(-2,0),由直线y=kx-2k,代入椭圆方程x2+4y2=4,运用韦达定理,可得B的坐标,再由中点的坐标公式可得AB的中点,设出Q(0,t),再由垂直平分线的概念可得k,t的关系式,运用向量的数量积的坐标表示可得k,t的一个关系式,解方程可得t,即可得到Q的坐标.
解答 解:(1)设A(x1,y1),B(x2,y2),
则$\overrightarrow{OA}$+$\overrightarrow{OB}$=(x1+x2,y1+y2),
联立直线y=kx+$\sqrt{5}$和椭圆方程x2+4y2=4,
可得(1+4k2)x2+8$\sqrt{5}$kx+16=0,
则△=64×5k2-64(1+4k2)>0,解得k>1或k<-1,
x1+x2=-$\frac{8\sqrt{5}k}{1+4{k}^{2}}$,y1+y2=k(x1+x1)+2$\sqrt{5}$=$\frac{2\sqrt{5}}{1+4{k}^{2}}$,
∴向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与$\overrightarrow{pQ}$=(-2,1)共线等价于x1+x2=-2(y1+y2),
即为-$\frac{8\sqrt{5}k}{1+4{k}^{2}}$=-2•$\frac{2\sqrt{5}}{1+4{k}^{2}}$,解得k=$\frac{1}{2}$,
不满足△>0,则不存在这样的常数k满足条件.
(2)椭圆C:$\frac{{x}^{2}}{4}$+y2=1的右焦点为($\sqrt{3}$,0),
设A(x1,y1),B(x2,y2),
由直线y=k(x-$\sqrt{3}$),代入椭圆方程x2+4y2=4,
可得(1+4k2)x2-8$\sqrt{3}$k2x+12k2-4=0,
即有x1+x2=$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{12{k}^{2}-4}{1+4{k}^{2}}$,①
又$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}B}$,可得$\sqrt{3}$-x1=2(x2-$\sqrt{3}$),②
联立①②,消去x1,x2,可得4k2=23,
解得k=±$\frac{\sqrt{23}}{2}$;
(3)椭圆的左顶点为A(-2,0),
由直线y=kx-2k,代入椭圆方程x2+4y2=4,
可得(1+4k2)x2+16k2x+16k2-4=0,
则-2•xB=$\frac{16{k}^{2}-4}{1+4{k}^{2}}$,即xB=$\frac{2-8{k}^{2}}{1+4{k}^{2}}$,
则B($\frac{2-8{k}^{2}}{1+4{k}^{2}}$,$\frac{4k}{1+4{k}^{2}}$),
AB中点的坐标为($\frac{1-4{k}^{2}}{1+4{k}^{2}}$-1,$\frac{2k}{1+4{k}^{2}}$),
设Q(0,t),由题意可得
$\frac{\frac{2k}{1+4{k}^{2}}-t}{\frac{-8{k}^{2}}{1+4{k}^{2}}}$=-$\frac{1}{k}$,化简为6k+t+4k2=0,①
由$\overrightarrow{QA}•\overrightarrow{QB}$=4,可得$\frac{16{k}^{2}-4}{1+4{k}^{2}}$+t2-$\frac{4kt}{1+4{k}^{2}}$=4,②
由①②解得k=$\frac{\sqrt{14}}{7}$,t=-$\frac{2\sqrt{14}}{5}$,或k=-$\frac{\sqrt{14}}{7}$,t=$\frac{2\sqrt{14}}{5}$.
即有Q的坐标为(0,±$\frac{2\sqrt{14}}{5}$).
点评 本题考查椭圆的方程和性质的运用,主要考查直线方程和椭圆方程联立,运用韦达定理和判别式,考查向量的共线及数量积的坐标表示,考查运算能力,属于中档题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | x+2y-8=0 | B. | x+2y+8=0 | C. | 2x-y-4=0 | D. | 2x-y+4=0 |
 设函数f(x)=|x2-2x|(x∈R).
设函数f(x)=|x2-2x|(x∈R).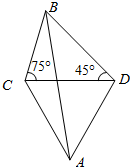 如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.