题目内容
(本小题满分12分,(Ⅰ)小题5分,(Ⅱ)小题7分)
设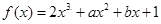 的导数为
的导数为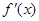 ,若函数
,若函数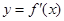 的图像关于直线
的图像关于直线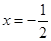 对称,且
对称,且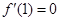 .
.
(Ⅰ)求实数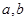 的值(Ⅱ)求函数
的值(Ⅱ)求函数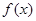 的极值
的极值
设
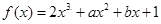 的导数为
的导数为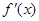 ,若函数
,若函数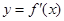 的图像关于直线
的图像关于直线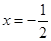 对称,且
对称,且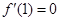 .
.(Ⅰ)求实数
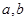 的值(Ⅱ)求函数
的值(Ⅱ)求函数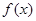 的极值
的极值(I)由题设条件知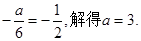 由于
由于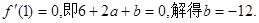
(II)函数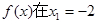 处取得极大值
处取得极大值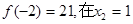 处取得极小值
处取得极小值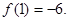
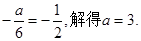 由于
由于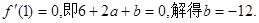
(II)函数
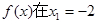 处取得极大值
处取得极大值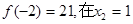 处取得极小值
处取得极小值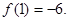
(I)由于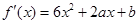 是二次函数,根据其对称轴为
是二次函数,根据其对称轴为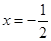 可求出a值,再利用
可求出a值,再利用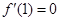 可求出b值.
可求出b值.
(II)在(I)的基础上可以利用导数研究其极值即可.要注意极大值和极小值的判断方法,左正右负为极大,左负右正为极小.
解:(I)因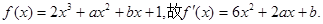
从而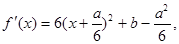 即
即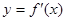 关于直线
关于直线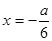 对称,从而由题设条件知
对称,从而由题设条件知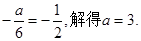
又由于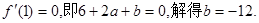 …………5分
…………5分
(II)由(I)知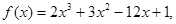
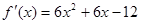
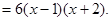
令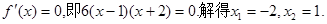
当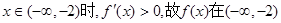 上为增函数;
上为增函数;
当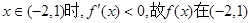 上为减函数;
上为减函数;
当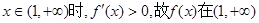 上为增函数;
上为增函数;
从而函数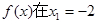 处取得极大值
处取得极大值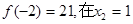 处取得极小值
处取得极小值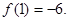 ……12 分
……12 分
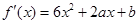 是二次函数,根据其对称轴为
是二次函数,根据其对称轴为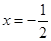 可求出a值,再利用
可求出a值,再利用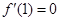 可求出b值.
可求出b值.(II)在(I)的基础上可以利用导数研究其极值即可.要注意极大值和极小值的判断方法,左正右负为极大,左负右正为极小.
解:(I)因
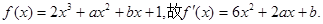
从而
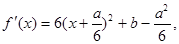 即
即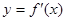 关于直线
关于直线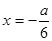 对称,从而由题设条件知
对称,从而由题设条件知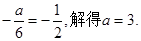
又由于
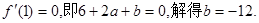 …………5分
…………5分(II)由(I)知
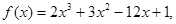
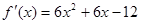
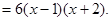
令
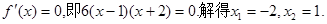
当
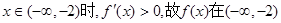 上为增函数;
上为增函数;当
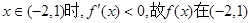 上为减函数;
上为减函数;当
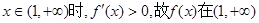 上为增函数;
上为增函数;从而函数
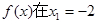 处取得极大值
处取得极大值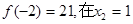 处取得极小值
处取得极小值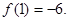 ……12 分
……12 分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
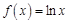 .
.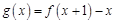 的最大值;
的最大值;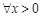 ,不等式
,不等式 恒成立,求实数
恒成立,求实数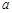 的取值范围;
的取值范围;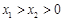 ,求证:
,求证: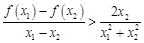 .
. ,
, .
. 的最大值;
的最大值;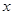 ,恒有
,恒有 成立,求实数
成立,求实数 的取值组成的集合.
的取值组成的集合. 时都取得极值.(1)求
时都取得极值.(1)求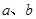 的值;
的值;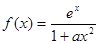 ,其中
,其中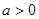
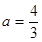 时,求
时,求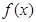 的极值点;
的极值点;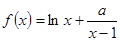 在
在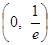 内有极值。
内有极值。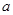 的取值范围;
的取值范围;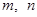 分别为
分别为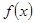 的极大值和极小值,记
的极大值和极小值,记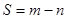 ,求S的取值范围。
,求S的取值范围。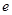 为自然对数的底数)
为自然对数的底数)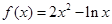 的递增区间是
的递增区间是 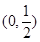
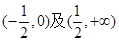
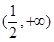
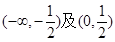
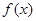 在定义域R内可导,若
在定义域R内可导,若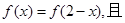
 ,若
,若 则
则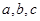 的大小关系是
的大小关系是



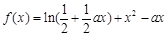 (
(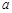 为常数,
为常数,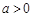 ).
).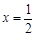 是函数
是函数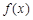 的一个极值点,求
的一个极值点,求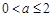 时,
时,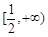 上是增函数;
上是增函数;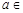 (1,2),总存在
(1,2),总存在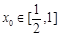 ,使不等式
,使不等式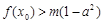 成立,求实数
成立,求实数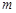 的取范围.
的取范围.