题目内容
17.在区间[-1,4]上随机取实数a,则方程x2+x+a=0存在实数根的概率为$\frac{1}{4}$.分析 由题意,本题是几何概型的考查,只要求出已知区间长度以及满足方程x2+x+a=0存在实数根的区间长度,由几何概型公式解答.
解答 解:区间[-1,4]长度为5,在此前提下满足方程x2+x+a=0存在实数根的a 的范围是1-4a≥0,解得区间是[-1,$\frac{1}{4}$],区间长度为:$\frac{5}{4}$,
由几何概型公式得到方程x2+x+a=0存在实数根的概率为:$\frac{\frac{5}{4}}{5}=\frac{1}{4}$;
故答案为:$\frac{1}{4}$.
点评 本题考查了几何概型概率的求法;关键是明确事件的测度是长度、面积还是体积,利用公式求概率.

练习册系列答案
相关题目
2.假设四边形ABCD为圆内接正方形,向圆内随机地投一点,则点落在正方形ABCD内的概率为( )
| A. | $\frac{\sqrt{2}}{2π}$ | B. | $\frac{1}{π}$ | C. | $\frac{\sqrt{2}}{π}$ | D. | $\frac{2}{π}$ |
6.一张长方形白纸,其厚度为a,面积为b,现将此纸对折(沿对边中点连线折叠)5次,这时纸的厚度和面积分别为( )
| A. | $\frac{1}{32}$a,32b | B. | 32a,$\frac{1}{32}b$ | C. | 16a,$\frac{1}{32}b$ | D. | 16a,$\frac{1}{16}b$ |
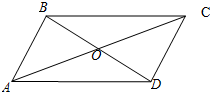 如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.