题目内容
8.已知函数f(x)=$\sqrt{{e}^{x}-a}$(e为自然对数的底数,a∈R),若存在x∈[0,1],使f(f(x))=x成立,则实数a的取值范围是[1,e-1].分析 利用反函数将问题进行转化,再将解方程问题转化为函数的图象交点问题.
解答 解:∵存在x∈[0,1],使f(f(x))=x成立,
∴存在x∈[0,1],使f(x)=f-1(x),
即函数f(x)与其反函数f-1(x)在[0,1]上有交点.
∵f(x)=$\sqrt{{e}^{x}-a}$(在[0,1]上为增函数,
∴函数f(x)与其反函数f-1(x)在[0,1]的交点在直线y=x上,
即函数f(x)与其反函数f-1(x)的交点就是f(x)与y=x的交点.
令$\sqrt{{e}^{x}-a}$=x,则方程在[0,1]上一定有解.
∴a=ex-x2,
设g(x)=ex-x2,
则g′(x)=ex-2x,令h(x)=ex-2x,h′(x)=ex-2,
当x>ln2时,h′(x)>0,当x<ln2时,h′(x)<0,
即有x=ln2处取得最小值2-2ln2>0,
即g′(x)>0在[0,1]上恒成立,
∴g(x)=ex-x2在[0,1]上递增,
∴a=g(x)≥g(0)=1,
g(x)≤g(1)=e-1;
综上可知,1≤a≤e-1.
故答案为:[1,e-1].
点评 本题主要考察了复合函数的性质,综合性较强,属于难题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
18.集合{Z|Z=in+i-n,n∈Z},用列举法表示该集合,这个集合是( )
| A. | {0,2,-2} | B. | {0,2} | C. | {0,2,-2,2i} | D. | {0,2,-2,2i,-2i} |
19.函数f(x)=sin2x,x∈R的一个对称中心是( )
| A. | ($\frac{π}{4}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{2}$,0) |
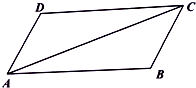 在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,
在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,