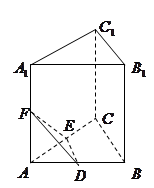题目内容
如图,储油灌的表面积 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.

⑴试用半径 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围.
⑵当圆柱高 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 最大?
最大?
 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
⑴试用半径
 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围.⑵当圆柱高
 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 最大?
最大?(1)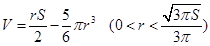 (2)
(2)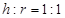
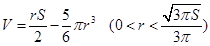 (2)
(2)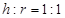
试题分析:(1)解决应用题问题首先要解决阅读问题,具体说就是要会用数学式子正确表示数量关系,本题先利用储油灌的表面积
 为定值得到圆柱高与半径的关系
为定值得到圆柱高与半径的关系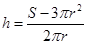 ,再根据储油灌的容积为半球体积与圆柱体积之和,即可得储油灌的容积
,再根据储油灌的容积为半球体积与圆柱体积之和,即可得储油灌的容积 的解析式;为使思路简洁,直接用对应公式表示,根据高及半径为正数可得
的解析式;为使思路简洁,直接用对应公式表示,根据高及半径为正数可得 的取值范围,(2)本题解题思路清晰,就是利用导数求最值.难点在运算上,需用字母
的取值范围,(2)本题解题思路清晰,就是利用导数求最值.难点在运算上,需用字母 表示高
表示高 与半径
与半径 .由导数为零得
.由导数为零得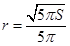 ,又由(1)得
,又由(1)得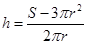 代入化简得
代入化简得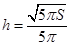 ,因此
,因此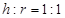 .
.试题解析:⑴
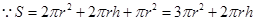 ,
,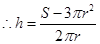 , 3分
, 3分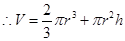
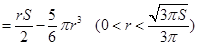 ; 7分
; 7分⑵
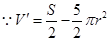 ,令
,令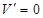 ,得
,得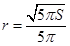 ,列表
,列表 | 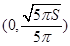 | 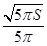 | 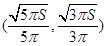 |
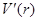 | 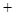 | 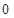 |  |
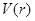 | ↗ | 极大值即最大值 | ↘ |
∴当
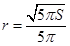 时,体积
时,体积 取得最大值,此时
取得最大值,此时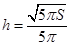 ,
,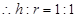 . 13分
. 13分答:储油灌容积
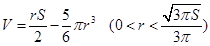 ,当
,当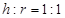 时容积
时容积 取得最大值. 15分
取得最大值. 15分
练习册系列答案
相关题目
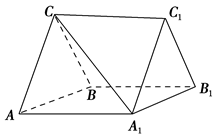
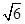 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积; π
π , 底面周长为3, 则这个球的体积为__________________.
, 底面周长为3, 则这个球的体积为__________________.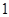 ,那么这个球的表面积为_______.
,那么这个球的表面积为_______.



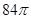 ,则圆台较小底面的面积为 .
,则圆台较小底面的面积为 . 种侧棱垂直于底面,
种侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱 中,
中, 分别是
分别是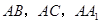 的中点,设三棱锥
的中点,设三棱锥 的体积为
的体积为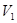 ,三棱柱
,三棱柱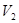 ,则
,则 .
.