题目内容
如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
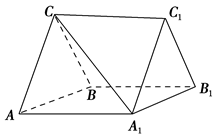
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=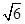 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.

(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=
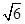 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.
(1)见解析(2)3(3)

(1)如图,取AB的中点O,连接CO,A1O.

∵CA=CB,∴CO⊥AB,
又∵AA1=AB,得AA1=2AO,
又∠A1AO=60°,
∴∠AOA1=90°,即AB⊥A1O,
∴AB⊥平面A1OC,又A1C?平面A1OC,
∴AB⊥A1C.
(2)∵AB=CB=2=AC,∴CO= ,
,
又A1A=AB=2,∠BAA1=60°,
∴在等边三角形AA1B中,A1O= ,
,
∵A1C2=A1O2+CO2=6,
∴∠COA1=90°,即A1O⊥CO,
∴A1O⊥平面ABC,
∴VABC-A1B1C1= ×22×
×22× =3.
=3.
(3)作辅助线同(1)
以O为原点,OA所在直线为x轴,OA1所在直线为y轴,OC所在直线为z轴,建立如图直角坐标系,则A(1,0,0),A1(0, ,0),B(-1,0,0),C(0,0,
,0),B(-1,0,0),C(0,0, ),B1(-2,
),B1(-2, ,0),则
,0),则 =(1,0,
=(1,0, ),
), =(-1,
=(-1, ,0),
,0), =(0,-
=(0,- ,
, ),设n=(x,y,z)为平面BB1C1C的法向量,则
),设n=(x,y,z)为平面BB1C1C的法向量,则 即
即 所以n=(
所以n=( ,1,-1),
,1,-1),
则cos<n, =
= =-
=- ,
,
所以A1C与平面BB1C1C所成角的正弦值为 .
.

∵CA=CB,∴CO⊥AB,
又∵AA1=AB,得AA1=2AO,
又∠A1AO=60°,
∴∠AOA1=90°,即AB⊥A1O,
∴AB⊥平面A1OC,又A1C?平面A1OC,
∴AB⊥A1C.
(2)∵AB=CB=2=AC,∴CO=
 ,
,又A1A=AB=2,∠BAA1=60°,
∴在等边三角形AA1B中,A1O=
 ,
,∵A1C2=A1O2+CO2=6,
∴∠COA1=90°,即A1O⊥CO,
∴A1O⊥平面ABC,
∴VABC-A1B1C1=
 ×22×
×22× =3.
=3.(3)作辅助线同(1)
以O为原点,OA所在直线为x轴,OA1所在直线为y轴,OC所在直线为z轴,建立如图直角坐标系,则A(1,0,0),A1(0,
 ,0),B(-1,0,0),C(0,0,
,0),B(-1,0,0),C(0,0, ),B1(-2,
),B1(-2, ,0),则
,0),则 =(1,0,
=(1,0, ),
), =(-1,
=(-1, ,0),
,0), =(0,-
=(0,- ,
, ),设n=(x,y,z)为平面BB1C1C的法向量,则
),设n=(x,y,z)为平面BB1C1C的法向量,则 即
即 所以n=(
所以n=( ,1,-1),
,1,-1),则cos<n,
 =
= =-
=- ,
,所以A1C与平面BB1C1C所成角的正弦值为
 .
.
练习册系列答案
相关题目
 A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF= AB.
AB.
 是圆柱体
是圆柱体 的一条母线,
的一条母线, 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 、
、 重合的任意一点,已知棱
重合的任意一点,已知棱 ,
, ,
, .
.
 ;
; 绕母线
绕母线 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积. 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 与半径
与半径 中,
中, 为线段
为线段 的中点,
的中点, .
.
 ⊥平面
⊥平面 ;
; 到平面
到平面 的距离.
的距离.  的半圆卷成一个圆锥,圆锥的体积为( )
的半圆卷成一个圆锥,圆锥的体积为( )



 ,这个正四棱锥的侧面积是________.
,这个正四棱锥的侧面积是________.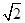 的正方体,则以该正方体各个面的中心为顶点的多面体的体积为________.
的正方体,则以该正方体各个面的中心为顶点的多面体的体积为________.