题目内容
10.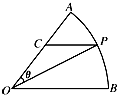 在扇形AOB中,圆心角等于$\frac{π}{3}$,半径为4,在弧AB上有一动点P(不与点AB重合),过点P引平行于OB的直线和OA交于点C,设∠AOP=θ,求三角形POC的面积的最大值及此时θ的值.
在扇形AOB中,圆心角等于$\frac{π}{3}$,半径为4,在弧AB上有一动点P(不与点AB重合),过点P引平行于OB的直线和OA交于点C,设∠AOP=θ,求三角形POC的面积的最大值及此时θ的值.
分析 根据CP∥OB求得∠CPO和和∠OCP进而在△POC中利用正弦定理求得PC和OC,进而利用三角形面积公式表示出S,利用两角和公式化简整理后,利用θ的范围确定三角形面积的最大值.
解答 解:因为CP∥OB,所以∠CPO=∠POB=60°-θ,∴∠OCP=120°.
在△POC中,由正弦定理得CP=$\frac{4sinθ}{sin120°}$=$\frac{8}{\sqrt{3}}$sinθ.OC=$\frac{4sin(60°-θ)}{sin120°}$=$\frac{8}{{\sqrt{3}}}sin({60°}-θ)$
三角形POC的面积S=$\frac{1}{2}$CP•OCsin120°=$\frac{1}{2}$•$\frac{8}{\sqrt{3}}$sinθ•$\frac{8}{{\sqrt{3}}}sin({60°}-θ)$•$\frac{\sqrt{3}}{2}$
=$\frac{8}{{\sqrt{3}}}sin(2θ+{30°})-\frac{{4\sqrt{3}}}{3}$,
所以当θ=30°,三角形POC的面积的最大值$\frac{{4\sqrt{3}}}{3}$.
点评 本题主要考查了三角函数的模型的应用.考查了考生分析问题和解决问题的能力.

练习册系列答案
相关题目
20.若随机变量X$~B(\;5\;,\;\frac{1}{3}\;)$,则P(X=2)=( )
| A. | ${(\frac{1}{3})^2}×{(\frac{2}{3})^3}$ | B. | ${(\frac{2}{3})^2}×{(\frac{1}{3})^3}$ | C. | $C_5^2{(\frac{2}{3})^2}×{(\frac{1}{3})^3}$ | D. | $C_5^2{(\frac{1}{3})^2}×{(\frac{2}{3})^3}$ |
1.若${({{x^2}-\frac{1}{ax}})^9}$(a∈R)的展开式中x9的系数是-$\frac{21}{2}$,则$\int_0^a{sinxdx}$的值为( )
| A. | 1-cos2 | B. | 2-cos1 | C. | cos2-1 | D. | 1+cos2 |
5. 如图是一个由圆、三角形、矩形组成的组合图,现用红黄两种颜色为其涂色,每个图形只涂一色,则三个颜色不全相同的概率是( )
如图是一个由圆、三角形、矩形组成的组合图,现用红黄两种颜色为其涂色,每个图形只涂一色,则三个颜色不全相同的概率是( )
 如图是一个由圆、三角形、矩形组成的组合图,现用红黄两种颜色为其涂色,每个图形只涂一色,则三个颜色不全相同的概率是( )
如图是一个由圆、三角形、矩形组成的组合图,现用红黄两种颜色为其涂色,每个图形只涂一色,则三个颜色不全相同的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
 如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆柱的母线长为6,底面半径为2,求该几何体的表面积.
如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆柱的母线长为6,底面半径为2,求该几何体的表面积.