题目内容
1．若${（{{x^2}-\frac{1}{ax}}）^9}$（a∈R）的展开式中x9的系数是-$\frac{21}{2}$，则$\int_0^a{sinxdx}$的值为（ ）| A． | 1-cos2 | B． | 2-cos1 | C． | cos2-1 | D． | 1+cos2 |
分析 先求出二项式展开式的通项公式，再令x的幂指数等于09，求得r的值，即可求得展开式中的x9的系数，再根据x9的系数为-$\frac{21}{2}$，求得a的值，从而求得$\int_0^a{sinxdx}$的值．
解答 解：${（{{x^2}-\frac{1}{ax}}）^9}$（a∈R）的展开式的通项公式为Tr+1=${C}_{9}^{r}$•${（-\frac{1}{a}）}^{r}$•x18-3r，
令18-3r=9，求得 r=3，可得展开式中x9的系数是-${C}_{9}^{3}$•a-3=-$\frac{21}{2}$，求得a=2，
可得 $\int_0^a{sinxdx}$=${∫}_{0}^{2}$sinxdx=-cosx${|}_{0}^{2}$=-（cos2-cos0）=1-cos2，
故选：A．
点评 本题主要考查定积分，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
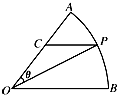在扇形AOB中，圆心角等于$\frac{π}{3}$，半径为4，在弧AB上有一动点P（不与点AB重合），过点P引平行于OB的直线和OA交于点C，设∠AOP=θ，求三角形POC的面积的最大值及此时θ的值．
11．设f（n）=2+24+27+210+…+23n+1（n∈N），则f（n）等于（ ）
| A． | $\frac{2}{7}$（8n-1） | B． | $\frac{2}{7}$（8n+1） | C． | $\frac{2}{7}$（8n+1-1） | D． | $\frac{2}{7}$（8n+1+1） |