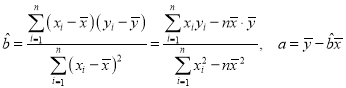题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)证明:![]() ,
,![]() 恒成立.
恒成立.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析
上单调递减;(2)证明见解析
【解析】
(1)可求得![]() ,分别在
,分别在![]() 、
、![]() 、
、![]() 、
、![]() 四种情况下讨论导函数的符号,从而得到原函数的单调性;(2)将不等式转化为:
四种情况下讨论导函数的符号,从而得到原函数的单调性;(2)将不等式转化为:![]() ,令
,令![]() ,
,![]() ,利用导数求得
,利用导数求得![]() 和
和![]() ,可证得
,可证得![]() ,从而证得结论.
,从而证得结论.
(1)![]() ,
,![]()
![]()
①当![]() 时,
时,![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
②当![]() 时,
时,![]()
![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
③当![]() 时,
时,![]()
![]() 在
在![]() 上恒成立
上恒成立
![]() 在
在![]() 上单调递增
上单调递增
④当![]() 时,
时,![]()
![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
综上所述:当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
(2)对![]() ,
,![]() 恒成立即为:
恒成立即为:![]() ,
,![]()
等价于:![]()
令![]() ,则
,则![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
![]()
令![]() ,则
,则![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
![]()
综上可得:![]() ,即
,即![]() 在
在![]() 上恒成立
上恒成立
![]() 对
对![]() ,
,![]() 恒成立
恒成立

【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
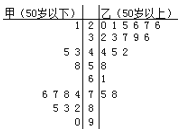
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
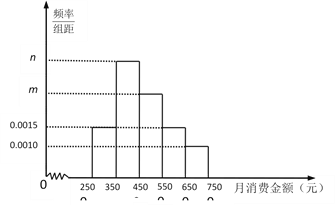
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来,我国大力发展新能源汽车工业,新能源汽车(含电动汽车)销量已跃居全球首位.某电动汽车厂新开发了一款电动汽车,并对该电动汽车的电池使用情况进行了测试,其中剩余电量![]() 与行驶时间
与行驶时间![]() (单位:小时)的测试数据如下:
(单位:小时)的测试数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如果剩余电量不足![]() ,则电池就需要充电.
,则电池就需要充电.
(1)从![]() 组数据中选出
组数据中选出![]() 组作回归分析,设
组作回归分析,设![]() 表示需要充电的数据组数,求
表示需要充电的数据组数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)根据电池放电的特点,剩余电量![]() 与时间
与时间![]() 工满足经验关系式:
工满足经验关系式:![]() ,通过散点图可以发现
,通过散点图可以发现![]() 与
与![]() 之间具有相关性.设
之间具有相关性.设![]() ,利用表格中的前
,利用表格中的前![]() 组数据求相关系数
组数据求相关系数![]()
![]() 的把握认为
的把握认为![]() 与
与![]() 之间具有线性相关关系.(当相关系数
之间具有线性相关关系.(当相关系数![]() 满足
满足![]() 时,则认为
时,则认为![]() 的把握认为两个变量具有线性相关关系);
的把握认为两个变量具有线性相关关系);
(3)利用![]() 与
与![]() 的相关性及前
的相关性及前![]() 组数据求出
组数据求出![]() 与工的回归方程.(结果保留两位小数)
与工的回归方程.(结果保留两位小数)
附录:相关数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
前9组数据的一些相关量:
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
|
|
|
|
|
相关公式:对于样本![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() ,相关系数
,相关系数 .
.