[题目]设双曲线的左.右焦点分别为. 若点P在双曲线上.且为锐角三角形.则|PF1|+|PF2|的取值范围是A. B. C. D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设双曲线的左、右焦点分别为. 若点P在双曲线上，且为锐角三角形，则|PF1|+|PF2|的取值范围是

A. B. C. D.

【答案】A

【解析】

由题意画出图形，不妨设P在第一象限，P点在P1与P2之间运动，求出∠PF2F1和∠F1PF2为直角时|PF1|+|PF2|的值，可得△F1PF2为锐角三角形时|PF1|+|PF2|的取值范围．

△F1PF2为锐角三角形，不妨设P在第一象限，P点在P1与P2之间运动，如图，

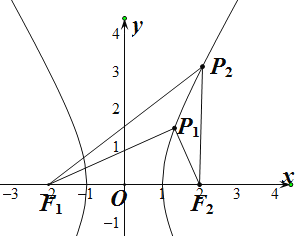
当P在P1处，∠F1P1F2为=90°，

∴S=|F1F2||y|=|P1F1||P1F2|，

由|P1F1|2+|P1F2|2=|F1F2|2，|P1F1|﹣|P1F2|=2，

可得|P1F1||P1F2|=6，

此时|P1F1|+|P1F2|=2，

当P在P2处，∠P2F1F2为=90°，x=2，

易知y=3，

此时|P2F1|+|P2F2|=2|P2F2|+2=8，

∴△F1PF2为锐角三角形，则|PF1|+|PF2|的取值范围是（2，8），

故选：A．

练习册系列答案

相关题目

【题目】写出下列命题的否定，并判断真假：

（1）不论取何实数，方程必有实数根；

（2）所有末位数字是0或5的整数都能被5整除；

（3）某些梯形的对角线互相平分；

（4）被8整除的数能被4整除．

【题目】李庄村某社区电费收取有以下两种方案供农户选择：

方案一：每户每月收管理费2元，月用电不超过30度，每度0.4元，超过30度时，超过部分按每度0.5元.

方案二：不收管理费，每度0.48元.

（1）求方案一收费元与用电量（度）间的函数关系；

（2）小李家九月份按方案一交费34元，问小李家该月用电多少度？

（3）小李家月用电量在什么范围时，选择方案一比选择方案二更好？

【题目】已知点P(x,y)在不等式组表示的平面区域内运动,则z=x-y的取值范围是(　　)

A. [-2,-1] B. [-2,1] C. [-1,2] D. [1,2]

【题目】已知函数，，.

（1）讨论函数的单调性；

（2）证明：，恒成立.

【题目】甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团，游戏规则为：

①先将一个圆8等分（如图），再将8个等分点，分别标注在8个相同的小球上，并将这8个小球放入一个不透明的盒子里，每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心构造三角形.若能构成直角三角形，则两个社团都参加；若能构成锐角三角形，则只参加美术社团；若能构成钝角三角形，则只参加音乐社团；若不能构成三角形，则两个社团都不参加.

②前一个同学摸出两个小球记录下结果后，把两个小球都放回盒内，下一位同学再从盒中随机摸取两个小球。

（1）求甲能参加音乐社团的概率；

（2）记甲、乙、丙3人能参加音乐社团的人数为随机变量，求的分布列、数学期望和方差

【题目】传说《西游记》中孙悟空的“如意金箍棒”原本是东海海底的一枚“定海神针”.作为兵器，“如意金箍棒”威力巨大，且只有孙悟空能让其大小随意变化。假定孙悟空在使用“如意金箍棒”与各路妖怪打斗时，都将其变化为底面半径为4至10之间的圆柱体。现假定孙悟空刚与一妖怪打斗完毕，并降伏了此妖怪，此时“如意金箍棒”的底面半径为10，长度为.在此基础上，孙悟空使“如意金箍棒”的底面半径以每秒1匀速缩短，同时长度以每秒40匀速增长，且在这一变化过程中，当“如意金箍棒”的底面半径为8时，其体积最大.