题目内容
17.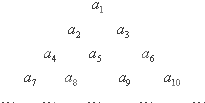 已知等差数列{an}中,a3=7,a6=16,将此等差数列的各项排成如下三角形数阵:则此数阵中第20行从左到右的第10个数是598.
已知等差数列{an}中,a3=7,a6=16,将此等差数列的各项排成如下三角形数阵:则此数阵中第20行从左到右的第10个数是598.
分析 先根据等差数列中的两项求出数列的通项,然后判定数阵中第20行从左到右的第10个数是该数列的第几项,从而求出所求.
解答 解:∵等差数列{an}中,a3=7,a6=16,
∴$\left\{\begin{array}{l}{a}_{1}+2d=7\\{a}_{1}+5d=16\end{array}\right.$,
解得$\left\{\begin{array}{l}{a}_{1}=1\\ d=3\end{array}\right.$,
而第行有1个数,第2行有2个数,依此类推第19行有19个数,
则第19行的最后一个数是数列的第1+2+…+19=190项,
则此数阵中第20行从左到右的第10个数是该数列的第200项,
∴a200=1+199×3=598.
故答案为:598
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
7.已知数列{an}为等比数列,a2=2,a5=$\frac{1}{4}$,则a1a2+a2a3+…+anan+1=( )
| A. | 16(1-$\frac{1}{{2}^{n}}$) | B. | 16(1-$\frac{1}{{4}^{n}}$) | C. | $\frac{32}{3}$(1-$\frac{1}{{2}^{n}}$) | D. | $\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$) |
12.为了解某班学生喜欢打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
下面的临界值表供参考:
则根据以下参考公式可得随机变量K2的值(保留三位小数),你认为有多大的把握认为喜爱打篮球与性别有关.(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15[ | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
6.设集合A={0,1,2,7},集合B={x|y=$\frac{2}{\sqrt{x-1}}$},则A∩B=( )
| A. | {1,2,7} | B. | {2,7} | C. | {0.1.2} | D. | {1,2} |
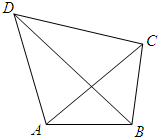 在四边形ABCD中,∠DAB与∠DCB互补,AB=1,CD=DA=2,对角线BD=$\sqrt{7}$,
在四边形ABCD中,∠DAB与∠DCB互补,AB=1,CD=DA=2,对角线BD=$\sqrt{7}$,