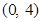题目内容
P是双曲线
-
=1的右支上一点,M.N分别是圆(x+10)2+y2=4和(x-10)2+y2=1上的点,则|PM|-|PN|的最大值为______.
| x2 |
| 36 |
| y2 |
| 64 |
双曲线
-
=1中,
∵a=6,b=8,c=10,
∴F1(-10,0),F2(10,0),
∵|PF1|-|PF2|=2a=12,
∴|MP|≤|PF1|+|MF1|,|PN|≥|PF2|+|NF2|,
∴-|PN|≤-|PF2|+|NF2|,
所以,|PM|-|PN|≤|PF1|+|MF1|-|PF2|+|NF2|
=12+1+2
=15.
故答案为:15.
| x2 |
| 36 |
| y2 |
| 64 |
∵a=6,b=8,c=10,
∴F1(-10,0),F2(10,0),
∵|PF1|-|PF2|=2a=12,
∴|MP|≤|PF1|+|MF1|,|PN|≥|PF2|+|NF2|,
∴-|PN|≤-|PF2|+|NF2|,
所以,|PM|-|PN|≤|PF1|+|MF1|-|PF2|+|NF2|
=12+1+2
=15.
故答案为:15.

练习册系列答案
相关题目
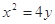 ,过点
,过点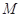
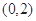 作直线与抛物线交于两点
作直线与抛物线交于两点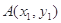 ,
,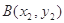 ,过
,过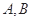 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为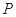 .
.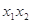 的值;
的值;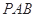 面积的最小值.
面积的最小值. 的抛物线方程为 .
的抛物线方程为 . 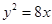 上一点P到
上一点P到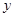 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )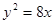 上的任意一点为圆心作圆与直线
上的任意一点为圆心作圆与直线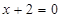 相切,这些圆必过一定点,则这一定点的坐标是( )
相切,这些圆必过一定点,则这一定点的坐标是( )