题目内容
9.执行如图的程序框图,当k的值为2015时,则输出的S值为( )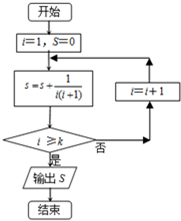
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
分析 模拟执行程序框图,可得程序框图的功能是计算并输出S=0+$\frac{1}{1×2}$+$\frac{1}{2×3}$$+\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$的值,用裂项法即可求值.
解答 解:模拟执行程序框图,可得
第一次循环,S=0+$\frac{1}{1×2}$,n=1<2015;
第二次循环,S=0+$\frac{1}{1×2}$+$\frac{1}{2×3}$,n=2<2015;
第二次循环,S=0+$\frac{1}{1×2}$+$\frac{1}{2×3}$$+\frac{1}{3×4}$,n=3<2015;
…
当n=2015时,S=0+$\frac{1}{1×2}$+$\frac{1}{2×3}$$+\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+$…+$\frac{1}{2015}$-$\frac{1}{2016}$=1-$\frac{1}{2016}$=$\frac{2015}{2016}$,
此时满足2015≥2015,退出循环,输出S的值为:$\frac{2015}{2016}$.
故选:C.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型⇒③解模.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若logm$\frac{1}{2}$<logn$\frac{1}{2}$<0,则( )
| A. | 1<m<n | B. | 1<n<m | C. | n<m<1 | D. | m<n<1 |
20.设a,b∈R,i是虚数单位,若a+1+bi=2-2i,则复数$\frac{a+bi}{a-bi}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.设实数x,y满足约束条件$\left\{\begin{array}{l}{2x-y+1≥0}\\{x+3y-3≥0}\\{x+y-2≤0}\end{array}\right.$,则z=$\frac{y}{x+1}$的取值范围是( )
| A. | [$\frac{1}{5}$,1] | B. | [$\frac{1}{5}$,$\frac{5}{4}$] | C. | [$\frac{1}{6}$,$\frac{3}{2}$] | D. | [$\frac{1}{6}$,$\frac{5}{4}$] |
14.已知集合M={x|2x-3<1},集合N={x|(x+1)(x-3)<0},则M∩N=( )
| A. | M | B. | N | C. | {x|-1<x<2} | D. | {x|x<3} |
1.已知f(x)=x3-1,设i是虚数单位,则复数$\frac{f(i)}{i}$的虚部为( )
| A. | -1 | B. | 1 | C. | i | D. | 0 |
18.设α∩β=m,直线a?α,直线b?β,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.下列有关命题的说法正确的是( )
| A. | p是q的必要不充分条件,则¬p是¬q的充分不必要条件 | |
| B. | 对于命题p:?x∈R,使得x+x-1<0,则¬p:?x∈R,均有x2+x-1>0 | |
| C. | 线性回归方程y=$\stackrel{∧}{b}$x+a对应的直线一定经过其样本数据点(x 1,y1)、(x2,y2)、…,(xn,yn) 中的一个 | |
| D. | “m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的充要条件 |