若logm$\frac{1}{2}$＜logn$\frac{1}{2}$＜0.则( )A．1＜m＜nB．1＜n＜mC．n＜m＜1D．m＜n＜1 题目和参考答案——青夏教育精英家教网——

题目内容

19．若log_m$\frac{1}{2}$＜log_n$\frac{1}{2}$＜0，则（　　）

A．

1＜m＜n

B．

1＜n＜m

C．

n＜m＜1

D．

m＜n＜1

分析利用对数的换底公式，将对数进行化简，然后利用对数函数的性质进行求解判断．

解答解：由换底公式可知，不等式log_m$\frac{1}{2}$＜log_n$\frac{1}{2}$＜0，等价为$\frac{1}{{log}_{\frac{1}{2}}m}＜\frac{1}{{log}_{\frac{1}{2}}n}＜0$，
则log$\frac{1}{2}$n＜log$\frac{1}{2}$m＜0，
∴n＞m＞1，即1＜m＜n．
故选：A．

点评本题主要考查对数的换底公式的应用，以及对数函数的单调性，倒数的性质，综合性较强．

练习册系列答案

课前课后同步练习系列答案

经纶学典课时作业系列答案

课堂小作业系列答案

黄冈小状元口算速算练习册系列答案

成功训练计划系列答案

倍速训练法直通中考考点系列答案

浙江名卷系列答案

励耘活页系列答案

一卷搞定系列答案

名校作业本系列答案

相关题目

9．已知直线l的参数方程为$\left\{{\begin{array}{l}{x=3t+2}\\{y=4t+3}\end{array}}\right.$（t为参数），圆C的极坐标方程为ρ=2cosθ，则圆C的圆心到直线l的距离等于1．

10．设（$\sqrt{3}$x-2）⁸=a₈x⁸+a₇x⁷+a₆x⁶+…+a₂x²+a₁x¹+a₀，则（a₈+a₆+a₄+a₂+a₀）²-（a₇+a₅+a₃+a₁）²=1．

7．已知e是自然对数的底数，函数f（x）=e^x（x²+5x-2），则f（x）的单调递减区间为[$\frac{-7-\sqrt{37}}{2}$，$\frac{-7+\sqrt{37}}{2}$]．

14．已知（2x-1）ⁿ展开式中，奇次项系数和比偶次项系数的和小3⁸，求C${\;}_{n}^{1}$+C${\;}_{n}^{2}$+C${\;}_{n}^{3}$+…+C${\;}_{n}^{n}$的值．

4．在平面直角坐标系xOy中，已知圆C₁：x²+y²=4，圆C₂：（x-2）²+y²=4．
（Ⅰ）在以O为极点，x轴正半轴为极轴的极坐标系中，分别求圆C₁与圆C₂的极坐标方程及两圆交点的极坐标；
（Ⅱ）求圆C₁与圆C₂的公共弦的参数方程．

11．在△ABC中，若$|{\overrightarrow{AB}}|=1$，$|{\overrightarrow{AC}}|=\sqrt{3}$，$|{\overrightarrow{AB}+\overrightarrow{AC}}|=|{\overrightarrow{BC}}|$，则$\frac{{\overrightarrow{AB}•\overrightarrow{BC}}}{{|{\overrightarrow{BC}}|}}$=（　　）

-$\frac{{\sqrt{3}}}{2}$

$\frac{{\sqrt{3}}}{2}$

8．在函数f（x）=alnx-（x-1）²的图象上，横坐标在区间（1，2）内变化的点处的切线斜率均大于1，则实数a的取值范围是（　　）

9．执行如图的程序框图，当k的值为2015时，则输出的S值为（　　）

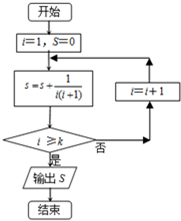
$\frac{2013}{2014}$

$\frac{2014}{2015}$

$\frac{2015}{2016}$

$\frac{2016}{2017}$