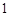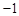题目内容
在等比数列{an} 中,若a6-a4=216,a3-a1=8,Sn=40,求q、a1及n.
设等比数列{an}的首项为a1,公比为q,由已知可知q≠1,
联立a6-a4=216,a3-a1=8,Sn=40,得:
,
由②得:q2-1=
④
把④代入①得,q3=27,所以,q=3.
把q=3代入④得,a1=1.
把a1=1,q=3代入③得:
=40
所以,3n=81,所以n=4.
联立a6-a4=216,a3-a1=8,Sn=40,得:
|
由②得:q2-1=
| 8 |
| a1 |
把④代入①得,q3=27,所以,q=3.
把q=3代入④得,a1=1.
把a1=1,q=3代入③得:
| 1×(1-3n) |
| 1-3 |
所以,3n=81,所以n=4.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
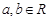 ,
,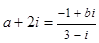 ,则
,则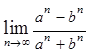 等于( ).
等于( ).