题目内容

{an}为等比数列，a2+a3=1，a3+a4=-2，则a5+a6+a7=（　　）
A．-24B．24C．-48D．48
设等比数列{an}的公比为q，
则q=
a3+a4
a2+a3
=-2，
故可得a2+a3=a1q+a1q2=2a1=1，即a1=
1
2

∴a5+a6+a7=a5（1+q+q2）=
1
2
×（-2）4（1-2+4）=24
故选B
练习册系列答案
相关题目
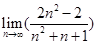已知{an}是等比数列，a6=2，a3=
1
4
，则公比q等于（　　）
A．-
1
2
B．-2C．2D．
1
2
等比数列{an}中已知a1+a2+a3=8，a4+a5+a6=-4，则S15=______．
已知{an}是各项均为正数的等比数列，且a1与a5的等比中项为2，则a2+a4的最小值等于______．
数列an的前n项和为Sn=2n+1-1，那么该数列前2n项中所有奇数位置的项的和为（　　）
A．
2
3
(4n-1)		B．
1
3
(22n+1+1)		C．
1
3
(4n-1)		D．
4
3
(4n-1)
在等比数列{an} 中，若a6-a4=216，a3-a1=8，Sn=40，求q、a1及n．
已知{an}满足a1=3，an+1=2an+1，
（1）求证：{an+1}是等比数列；
（2）求这个数列的通项公式an．
在等比数列{an}中，已知a1=
3
2
，a4=12，则q=______；an=______．
计算极限：=         ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网