题目内容

设等比数列{an}中，a3是a1，a2的等差中项，则数列的公比为______．
设等比数列{an}的公比为q，
则：a2=a1q，a3=a1q2，
由a3是a1，a2的等差中项，
得：2a3=a1+a2，即2a1q2=a1+a1q，
因为a1≠0，所以2q2-q-1=0，解得：q=-
1
2
或q=1．
故答案为-
1
2
或1．
练习册系列答案
相关题目
在等比数列{an}中，公比q=-2，S5=44，则a1的值为（　　）
A．4B．-4C．2D．-2
已知{an}是各项均为正数的等比数列，且a1与a5的等比中项为2，则a2+a4的最小值等于______．
在等比数列{an} 中，若a6-a4=216，a3-a1=8，Sn=40，求q、a1及n．
已知{an}满足a1=3，an+1=2an+1，
（1）求证：{an+1}是等比数列；
（2）求这个数列的通项公式an．
某企业在1996年初贷款M万元，年利率为m，从该年末开始，每年偿还的金额都是a万元，并恰好在10年间还清，则a的值等于（　　）
A．
M(1+m)10
(1+m)10-1
B．
Mm
(1+m)10
C．
Mm(1+m)10
(1+m)10-1
D．
Mm
(1+m)10-1
在等比数列{an}中，已知a1=
3
2
，a4=12，则q=______；an=______．
数列{bn}(n∈N*)是递增的等比数列，且b1+b3=5，b1b3=4，
（1）求数列{bn}的通项公式；
（2）若an=log2bn+3，求证：数列{an}是等差数列．
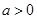设常数，展开式中的系数为，则______ 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网