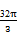题目内容
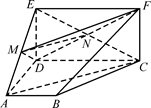
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°, ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.

 ,M是线段AE上的动点.
,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.

(1)见解析
(2)1:4
(2)1:4
(1)当M是线段AE的中点时,AC∥平面MDF.证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN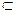 平面MDF,又AC
平面MDF,又AC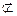 平面MDF,
平面MDF,
所以AC∥平面MDF.
(2)如图,将几何体ADE-BCF补成三棱柱ADE-B¢CF,
三棱柱ADE-B¢CF的体积为 ,
,
则几何体ADE-BCF的体积
 =
= .
.
三棱锥F-DEM的体积V三棱锥M-DEF=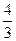 ,
,
故两部分的体积之比为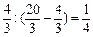 (答1:4,4,4:1均可).
(答1:4,4,4:1均可).
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN
 平面MDF,又AC
平面MDF,又AC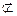 平面MDF,
平面MDF,所以AC∥平面MDF.
(2)如图,将几何体ADE-BCF补成三棱柱ADE-B¢CF,

三棱柱ADE-B¢CF的体积为
 ,
,则几何体ADE-BCF的体积
 =
= .
.三棱锥F-DEM的体积V三棱锥M-DEF=
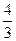 ,
,故两部分的体积之比为
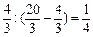 (答1:4,4,4:1均可).
(答1:4,4,4:1均可).
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
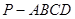 中,底面
中,底面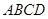 是边长为
是边长为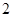 的正方形,侧棱
的正方形,侧棱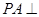 底面
底面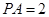 ,
,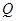 是
是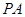 的中点.
的中点.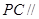 平面
平面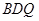 ;
;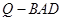 的体积.
的体积.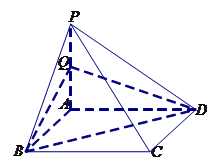
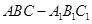 中,平面
中,平面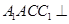 平面ABC,
平面ABC,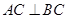 ,
,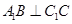 ,
,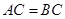 .
.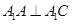 ;
;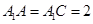 ,求三棱锥
,求三棱锥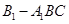 的体积.
的体积.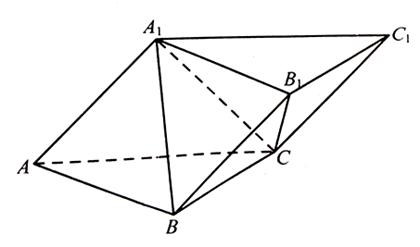
 中,底面ABCD和侧面
中,底面ABCD和侧面 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,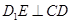 ,
, .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.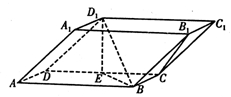
 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过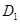 、E、F作平面
、E、F作平面 交
交 于G.
于G. ;
; 的余弦值;
的余弦值; 的体积.
的体积.

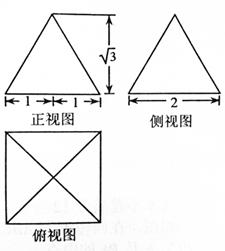
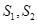 ,体积为
,体积为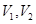 ,若它们的侧面积相等且
,若它们的侧面积相等且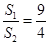 ,则
,则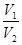 的值是 .
的值是 .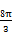
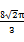
 π
π