题目内容
(满分12分)直线l 与抛物线y2 = 4x 交于两点A、B,O 为原点,且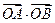 = -4.
= -4.
(I) 求证:直线l 恒过一定点;
(II) 若 4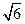 ≤| AB | ≤
≤| AB | ≤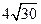 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围;
(Ⅲ) 设抛物线的焦点为F,∠AFB = θ,试问θ 角 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.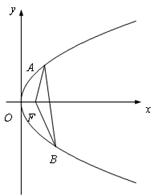
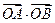 = -4.
= -4.(I) 求证:直线l 恒过一定点;
(II) 若 4
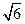 ≤| AB | ≤
≤| AB | ≤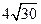 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围;(Ⅲ) 设抛物线的焦点为F,∠AFB = θ,试问θ 角
 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
(Ⅰ)见解析
(Ⅱ) kÎ [-1, -]∪[ , 1 ].
(Ⅲ)见解析
(Ⅱ) kÎ [-1, -]∪[ , 1 ].
(Ⅲ)见解析
(I) 1°若直线l 与x 轴不垂直,
设其方程为y = kx + b,l 与抛物线y2 = 4x 的交点坐标分别为A(x1, y1)、B(x2, y2),
由·= -4 得x1x2 + y1y2 = -4,即+ y1y2 = -4,
则y1y2 = -8. 1分
又由得ky2-4y + 4b =" 0" (k≠ 0).
则y1y2 = = -8,即b = -2k, 2分]
则直线l 的方程为y = k (x-2),则直线l 过定点 (2, 0). 3分
2°若直线l⊥x 轴,易得x1 = x2 = 2,则l 也过定点 (2, 0).
综上,直线l 恒过定点 (2, 0). 4分
(II) 由 (I) 得 | AB | 2 =" (1" + )(y2-y1) 2 = ( + 32) 6分
从而 6 ≤( + 2) ≤ 30. 7分
解得kÎ [-1, -]∪[ , 1 ]. 8分
 (III) 假定θ = p,则有cosθ = -,
(III) 假定θ = p,则有cosθ = -,
如图,即= - (*) 9分
由 (I) 得y1y2 = -8,x1x2 = = 4.
由定义得 | AF | = x1 + 1,| BF | = x2 + 1.
从而有 | AF | 2 + | BF | 2-| AB | 2 = (x1 + 1) 2 + (x2 + 1) 2-(x1-x2) 2-(y1-y2) 2
= -2 (x1 + x2)-6, 12分
| AF |·| BF | = (x1 + 1) (x2 + 1) = x1x2 + x1 + x2 + 1 = x1 + x2 + 5
将代入 (*) 得= -,即x1 + x2 + 1 = 0.
这与x1 > 0 且x2 > 0 相矛盾! 13分
经检验,当AB⊥x 轴时,θ =" 2" arctan 2> p.
综上,θ≠p. 14分
设其方程为y = kx + b,l 与抛物线y2 = 4x 的交点坐标分别为A(x1, y1)、B(x2, y2),
由·= -4 得x1x2 + y1y2 = -4,即+ y1y2 = -4,
则y1y2 = -8. 1分
又由得ky2-4y + 4b =" 0" (k≠ 0).
则y1y2 = = -8,即b = -2k, 2分]
则直线l 的方程为y = k (x-2),则直线l 过定点 (2, 0). 3分
2°若直线l⊥x 轴,易得x1 = x2 = 2,则l 也过定点 (2, 0).
综上,直线l 恒过定点 (2, 0). 4分
(II) 由 (I) 得 | AB | 2 =" (1" + )(y2-y1) 2 = ( + 32) 6分
从而 6 ≤( + 2) ≤ 30. 7分
解得kÎ [-1, -]∪[ , 1 ]. 8分
 (III) 假定θ = p,则有cosθ = -,
(III) 假定θ = p,则有cosθ = -,如图,即= - (*) 9分
由 (I) 得y1y2 = -8,x1x2 = = 4.
由定义得 | AF | = x1 + 1,| BF | = x2 + 1.
从而有 | AF | 2 + | BF | 2-| AB | 2 = (x1 + 1) 2 + (x2 + 1) 2-(x1-x2) 2-(y1-y2) 2
= -2 (x1 + x2)-6, 12分
| AF |·| BF | = (x1 + 1) (x2 + 1) = x1x2 + x1 + x2 + 1 = x1 + x2 + 5
将代入 (*) 得= -,即x1 + x2 + 1 = 0.
这与x1 > 0 且x2 > 0 相矛盾! 13分
经检验,当AB⊥x 轴时,θ =" 2" arctan 2> p.
综上,θ≠p. 14分

练习册系列答案
相关题目
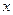 轴,焦点
轴,焦点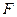 在直线
在直线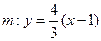 上,直线
上,直线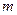 与抛物线相交于
与抛物线相交于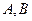 两点,
两点,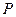 为抛物线上一动点(不同于
为抛物线上一动点(不同于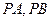 分别交该抛物线的准线
分别交该抛物线的准线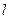 于点
于点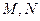 。
。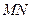 为直径的圆
为直径的圆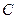 经过焦点
经过焦点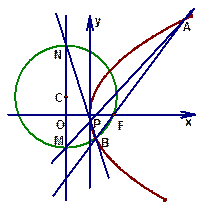
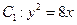 与双曲线
与双曲线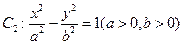 有公共焦点
有公共焦点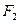 ,点
,点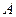 是曲线
是曲线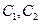 在第一象限的交点,且
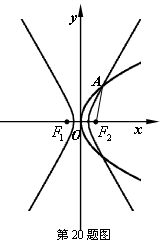
在第一象限的交点,且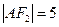 .
.
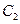 的方程;
的方程;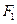 为圆心的圆
为圆心的圆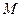 与双曲线的一条渐近线相切,
与双曲线的一条渐近线相切,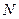 :
: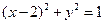 .已知点
.已知点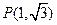 ,过点
,过点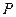 作互相垂
作互相垂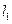 和
和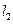 ,设
,设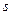 ,
,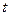 .
.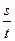 是否为定值?
是否为定值?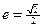 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线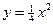 的焦点重合.
的焦点重合. ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
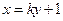 所经过的定点
所经过的定点 恰好是椭圆
恰好是椭圆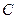 的一个焦点,且椭圆
的一个焦点,且椭圆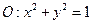 ,直线
,直线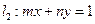 .试证明:当点
.试证明:当点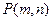 在椭圆
在椭圆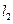 与圆
与圆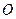 恒相交,并求直线
恒相交,并求直线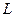 的取值范围.
的取值范围.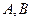 两点,若直线
两点,若直线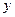 轴于点
轴于点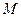 ,且
,且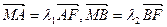 ,当
,当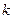 变化时,求
变化时,求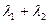 的值;
的值; 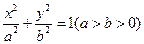 经过点
经过点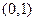 ,过右焦点F且不与x轴重合的动直线L交椭圆于
,过右焦点F且不与x轴重合的动直线L交椭圆于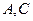 两点,当动直线L的斜率为2时,坐标原点O到L的距离为
两点,当动直线L的斜率为2时,坐标原点O到L的距离为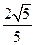 .
.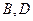 两点,且
两点,且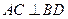 ,当四边形
,当四边形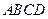 的面积S=
的面积S=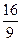 时,求直线L的方程.
时,求直线L的方程.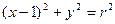 与椭圆
与椭圆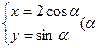 为参数)有公共点,则圆的半径的取值范围是
为参数)有公共点,则圆的半径的取值范围是
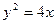 的焦点是双曲线
的焦点是双曲线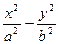 =1(
=1(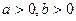 )的右顶点,双曲线的其中一条渐近线方程为
)的右顶点,双曲线的其中一条渐近线方程为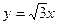 ,则双曲线的离心率为________。
,则双曲线的离心率为________。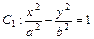 (a>0,b>0)的左准线为l,左、右焦点分别为F1、F2,抛物线C2的准线为l,焦点为F2,C1与C2的交点为M,则
(a>0,b>0)的左准线为l,左、右焦点分别为F1、F2,抛物线C2的准线为l,焦点为F2,C1与C2的交点为M,则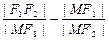 = 。
= 。