题目内容
(13分)已知椭圆C的中心在坐标原点,离心率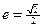 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线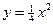 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)过点S(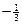 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
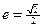 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线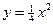 的焦点重合.
的焦点重合.(1)求椭圆C的方程;
(2)过点S(
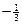 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.x2+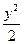 =1,存在一个定点T(1,0)满足条件
=1,存在一个定点T(1,0)满足条件
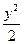 =1,存在一个定点T(1,0)满足条件
=1,存在一个定点T(1,0)满足条件解:(Ⅰ)设椭圆的方程为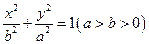 ,离心率
,离心率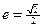 ,
,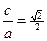 ,抛物线
,抛物线 的焦点为
的焦点为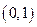 ,所以
,所以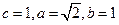 ,椭圆C的方程是x2+
,椭圆C的方程是x2+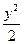 =1.…………(4分)
=1.…………(4分)
(Ⅱ)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1,若直线l垂直于x轴,则以AB为直径的圆是(x+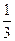 )2+y2=
)2+y2=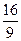 .网
.网
由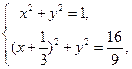 解得
解得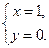 即两圆相切于点(1,0).网
即两圆相切于点(1,0).网
因此所求的点T如果存在,只能是(1,0).…………(6分)网
事实上,点T(1,0)就是所求的点.证明如下:
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0).
若直线l不垂直于x轴,可设直线l:y=k(x+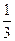 ).网
).网
由 即(k2+2)x2+
即(k2+2)x2+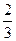 k2x+
k2x+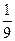 k2-2=0.网
k2-2=0.网
记点A(x1,y1),B(x2,y2),则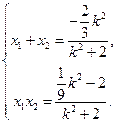 …………(9分网)
…………(9分网)
又因为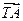 =(x1-1, y1),
=(x1-1, y1), 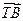 =(x2-1, y2),
=(x2-1, y2),
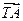 ·
·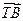 =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+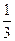 )(x2+
)(x2+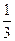 )网
)网
=(k2+1)x1x2+(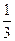 k2-1)(x1+x2)+
k2-1)(x1+x2)+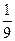 k2+1网
k2+1网
=(k2+1)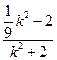 +(
+(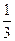 k2-1)
k2-1) 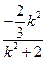 +
+ 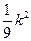 +1=0,网
+1=0,网
所以TA⊥TB,即以AB为直径的圆恒过点T(1,0).
所以在坐标平面上存在一个定点T(1,0)满足条件. …………(13分)
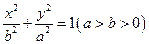 ,离心率
,离心率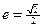 ,
,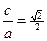 ,抛物线
,抛物线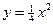 的焦点为
的焦点为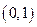 ,所以
,所以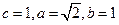 ,椭圆C的方程是x2+
,椭圆C的方程是x2+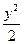 =1.…………(4分)
=1.…………(4分)(Ⅱ)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1,若直线l垂直于x轴,则以AB为直径的圆是(x+
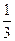 )2+y2=
)2+y2=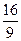 .网
.网由
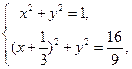 解得
解得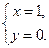 即两圆相切于点(1,0).网
即两圆相切于点(1,0).网因此所求的点T如果存在,只能是(1,0).…………(6分)网
事实上,点T(1,0)就是所求的点.证明如下:
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0).
若直线l不垂直于x轴,可设直线l:y=k(x+
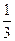 ).网
).网由
 即(k2+2)x2+
即(k2+2)x2+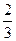 k2x+
k2x+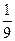 k2-2=0.网
k2-2=0.网记点A(x1,y1),B(x2,y2),则
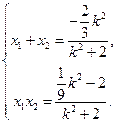 …………(9分网)
…………(9分网)又因为
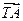 =(x1-1, y1),
=(x1-1, y1), 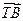 =(x2-1, y2),
=(x2-1, y2),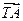 ·
·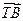 =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+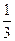 )(x2+
)(x2+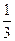 )网
)网=(k2+1)x1x2+(
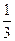 k2-1)(x1+x2)+
k2-1)(x1+x2)+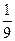 k2+1网
k2+1网=(k2+1)
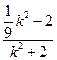 +(
+(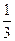 k2-1)
k2-1) 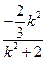 +
+ 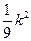 +1=0,网
+1=0,网所以TA⊥TB,即以AB为直径的圆恒过点T(1,0).
所以在坐标平面上存在一个定点T(1,0)满足条件. …………(13分)

练习册系列答案
相关题目
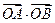 = -4.
= -4.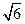 ≤| AB | ≤
≤| AB | ≤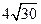 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围; 能否
能否
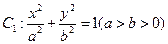 的长轴长为
的长轴长为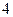 ,离心率为
,离心率为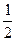 ,
,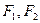 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点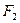 ,且与直线
,且与直线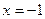 相切.
相切.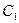 的方程; (ⅱ)求动圆圆心轨迹
的方程; (ⅱ)求动圆圆心轨迹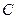 的方程;
的方程;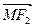 与
与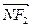 共线,
共线,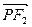 与
与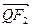 共线,且
共线,且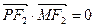 ,求四边形
,求四边形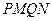 面积的最小值.
面积的最小值.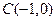 及椭圆
及椭圆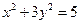 ,过点
,过点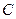 的动直线与该椭圆相交于
的动直线与该椭圆相交于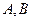 两点.
两点.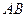 中点的横坐标是
中点的横坐标是 ,求直线
,求直线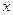 轴上是否存在点
轴上是否存在点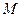 ,使
,使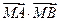 为常数?若存在,求出点
为常数?若存在,求出点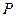 过点
过点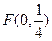 且与直线
且与直线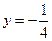 相切.
相切.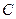 的方程;
的方程;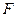 作一条直线交轨迹
作一条直线交轨迹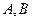 两点,轨迹
两点,轨迹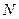 ,
,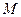 为线段
为线段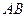 的中点,求证:
的中点,求证: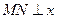 轴.
轴.
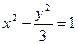 的右焦点
的右焦点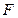 作倾斜角为
作倾斜角为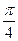 的直线交双曲线于A、B两点,
的直线交双曲线于A、B两点, 与曲线
与曲线 只有一个交点,则实数
只有一个交点,则实数
 .
.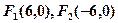 ,并且过点
,并且过点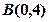 ,则该双曲线的渐近线方程为 ( )
,则该双曲线的渐近线方程为 ( ) 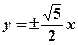


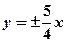
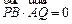 ,则双曲线C的离心率e= .
,则双曲线C的离心率e= .