题目内容
(本小题满分12分)已知直线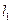
 所经过的定点
所经过的定点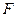 恰好是椭圆
恰好是椭圆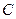 的一个焦点,且椭圆
的一个焦点,且椭圆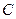 上的点到点
上的点到点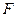 的最大距离为3.
的最大距离为3.
(Ⅰ)求椭圆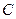 的标准方程;
的标准方程;
(Ⅱ)已知圆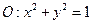 ,直线
,直线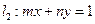 .试证明:当点
.试证明:当点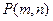 在椭圆
在椭圆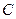 上运动时,直线
上运动时,直线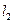 与圆
与圆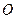 恒相交,并求直线
恒相交,并求直线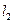 被圆
被圆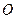 所截得弦长
所截得弦长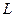 的取值范围.
的取值范围.
(Ⅲ)设直线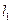 与椭圆交于
与椭圆交于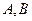 两点,若直线
两点,若直线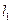 交
交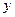 轴于点
轴于点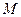 ,且
,且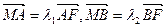 ,当
,当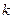 变化时,求
变化时,求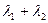 的值;
的值;
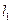
 所经过的定点
所经过的定点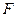 恰好是椭圆
恰好是椭圆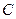 的一个焦点,且椭圆
的一个焦点,且椭圆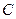 上的点到点
上的点到点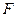 的最大距离为3.
的最大距离为3.(Ⅰ)求椭圆
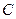 的标准方程;
的标准方程;(Ⅱ)已知圆
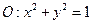 ,直线
,直线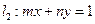 .试证明:当点
.试证明:当点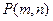 在椭圆
在椭圆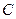 上运动时,直线
上运动时,直线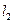 与圆
与圆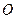 恒相交,并求直线
恒相交,并求直线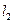 被圆
被圆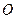 所截得弦长
所截得弦长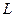 的取值范围.
的取值范围.(Ⅲ)设直线
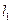 与椭圆交于
与椭圆交于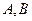 两点,若直线
两点,若直线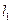 交
交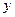 轴于点
轴于点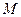 ,且
,且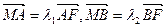 ,当
,当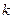 变化时,求
变化时,求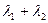 的值;
的值; (1)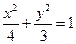 (2)
(2)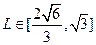 (3)
(3)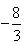
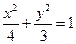 (2)
(2)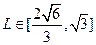 (3)
(3)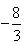
(Ⅰ)由 得,所以直线过定点(1,0),即
得,所以直线过定点(1,0),即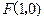 .
.
设椭圆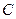 的方程为
的方程为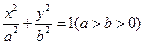 ,
,
则 ,解得
,解得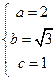 ,所以椭圆
,所以椭圆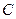 的方程为
的方程为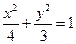 . …………3分
. …………3分
(Ⅱ)因为点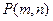 在椭圆
在椭圆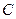 上运动,所以
上运动,所以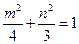 ,
,
从而圆心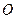 到直线
到直线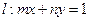 的距离
的距离
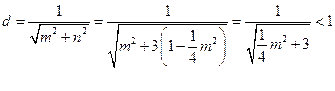
所以直线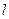 与圆
与圆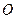 恒相交. ……………………5分
恒相交. ……………………5分
又直线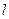 被圆
被圆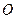 截得的弦长
截得的弦长
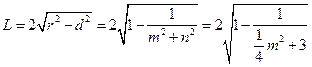 , …………6分
, …………6分
由于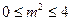 ,所以
,所以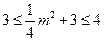 ,则
,则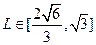 ,
,
即直线 被圆
被圆 截得的弦长的取值范围是
截得的弦长的取值范围是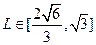 . …………………7分
. …………………7分
(3)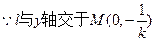 设
设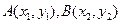
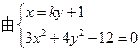
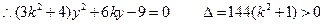
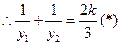 …………………………9分
…………………………9分
又由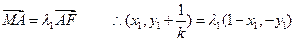
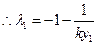 同理
同理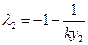 ………………………………11分
………………………………11分
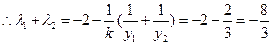 ………………………12分
………………………12分
 得,所以直线过定点(1,0),即
得,所以直线过定点(1,0),即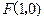 .
. 设椭圆
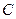 的方程为
的方程为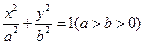 ,
, 则
 ,解得
,解得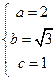 ,所以椭圆
,所以椭圆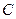 的方程为
的方程为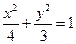 . …………3分
. …………3分(Ⅱ)因为点
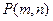 在椭圆
在椭圆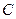 上运动,所以
上运动,所以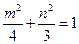 ,
, 从而圆心
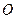 到直线
到直线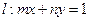 的距离
的距离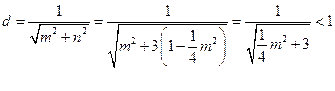
所以直线
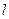 与圆
与圆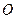 恒相交. ……………………5分
恒相交. ……………………5分又直线
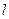 被圆
被圆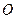 截得的弦长
截得的弦长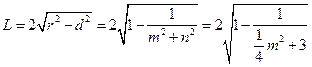 , …………6分
, …………6分由于
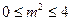 ,所以
,所以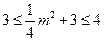 ,则
,则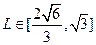 ,
,即直线
 被圆
被圆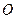 截得的弦长的取值范围是
截得的弦长的取值范围是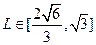 . …………………7分
. …………………7分(3)
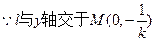 设
设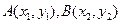
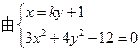
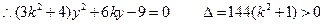
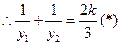 …………………………9分
…………………………9分又由
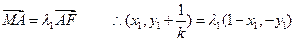
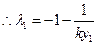 同理
同理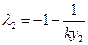 ………………………………11分
………………………………11分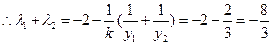 ………………………12分
………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
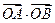 = -4.
= -4. ≤| AB | ≤
≤| AB | ≤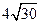 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围; 能否
能否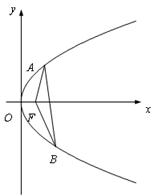
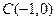 及椭圆
及椭圆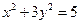 ,过点
,过点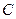 的动直线与该椭圆相交于
的动直线与该椭圆相交于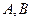 两点.
两点.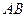 中点的横坐标是
中点的横坐标是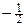 ,求直线
,求直线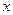 轴上是否存在点
轴上是否存在点 ,使
,使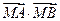 为常数?若存在,求出点
为常数?若存在,求出点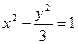 的右焦点
的右焦点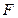 作倾斜角为
作倾斜角为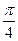 的直线交双曲线于A、B两点,
的直线交双曲线于A、B两点,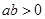 ”是“方程
”是“方程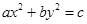 表示椭圆”的 ( )
表示椭圆”的 ( )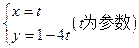 与抛物线
与抛物线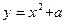 交于A、B两点,则实数
交于A、B两点,则实数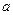 的取值范围是 .
的取值范围是 . 的一个焦点
的一个焦点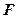 作圆
作圆 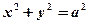 的两条切线,切点分别为A,B,若
的两条切线,切点分别为A,B,若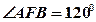 ,则双曲线C的离心率为 。
,则双曲线C的离心率为 。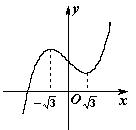
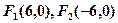 ,并且过点
,并且过点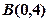 ,则该双曲线的渐近线方程为 ( )
,则该双曲线的渐近线方程为 ( ) 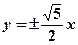
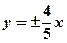
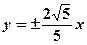
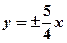
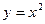 在点(1,1)处的切线方程为 。
在点(1,1)处的切线方程为 。