题目内容
设定义在[a,b](a≥-4)上的函数f(x),若函数g(x)=f(
+2m)与f(x)的定义域与值域都相同,则实数m的取值范围为______.
| x+4 |
令t=
+2m,由题意知函数t=
+2m的定义域与值域均为[a,b](a≥-4)
又函数t=
+2m在定义域内为增函数,所以
,即方程
+2m=x在区间[-4,+∞)内有两个不等的根.
如图,构造函数y=
,y=x-2m则可知直线与抛物线相切时,两函数图象有一个交点,过点(-4,0)时,有两个交点.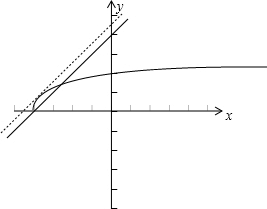
当直线与抛物线相切时,
=x-2m,∴x2-(4m+1)x+4m2-4=0,
∴△=(4m+1)2-4(4m2-4)=0,∴m=-
当直线过点(-4,0)时,-4-2m=0,∴m=-2
根据图象可知,实数m的取值范围为(-
,-2]
故答案为:(-
,-2]
| x+4 |
| x+4 |
又函数t=
| x+4 |
|
| x+4 |
如图,构造函数y=
| x+4 |

当直线与抛物线相切时,
| x+4 |
∴△=(4m+1)2-4(4m2-4)=0,∴m=-
| 17 |
| 8 |
当直线过点(-4,0)时,-4-2m=0,∴m=-2
根据图象可知,实数m的取值范围为(-
| 17 |
| 8 |
故答案为:(-
| 17 |
| 8 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
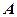 =
=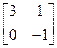 ,求
,求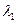 ,
,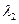 及对应的特征向量
及对应的特征向量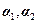 .
.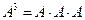 ,若矩阵
,若矩阵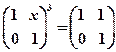 ,则
,则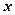 的值是_____________.
的值是_____________.