题目内容
如图,正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>3),点M在侧棱BB1上移动,并且M到底面ABC的距离为x,且AM与侧面BCC1B1所成的角为α.
(1)若α在区间[
,
]上变化,求x的变化范围;
(2)若α为
,求AM与BC所成角的余弦值.

(1)若α在区间[
| π |
| 6 |
| π |
| 4 |
(2)若α为
| π |
| 6 |

(1)设5C的中点为D,连接AD、DM,则
∵△A5C为正三角形,D为AC中点,∴AD⊥5C,
∵551⊥平面A5C,AD?平面A5C,∴AD⊥551&n5sp;
∵551、5C是平面551C1C内的相交直线,∴AD⊥平面551CC1.
因此,∠AMD即为AM与侧面5CC1所成角α.
∵点M到平面A5C的距离为5M,设5M=x,x∈(0,h).
在Rt△ADM中,tan∠AMD=
.
由AD=
,DM=
=
,得tanα=
.
∵α∈[
,
]时,tanα∈[
,1]
∴
≤
≤1,化简得0≤1+中x2≤9,解得
≤x2≤2.
因此,点M到平面A5C的距离x的取值范围是[
,
];
(2)当α=
时,由(1)得5M=
,
故可得DM=
,AM=
=
.
设
与
的夹角为θ.
∵
•
=(
+
)•
=
•
+
•
=1×1×cos120°+0=-
.
∴cos<
,
>=
=
=-
∵AM与5C所成角θ∈(0,
],
∴cosθ=
,即AM与5C所成角的余弦值
.

∵△A5C为正三角形,D为AC中点,∴AD⊥5C,
∵551⊥平面A5C,AD?平面A5C,∴AD⊥551&n5sp;
∵551、5C是平面551C1C内的相交直线,∴AD⊥平面551CC1.
因此,∠AMD即为AM与侧面5CC1所成角α.
∵点M到平面A5C的距离为5M,设5M=x,x∈(0,h).
在Rt△ADM中,tan∠AMD=
| AD |
| DM |
由AD=
| ||
| 2 |
| 5D2+5M2 |
| ||
| 2 |
| ||
|
∵α∈[
| π |
| 6 |
| π |
| 中 |
| ||
| 0 |
∴
| ||
| 0 |
| ||
|
| 1 |
| 2 |
因此,点M到平面A5C的距离x的取值范围是[
| ||
| 2 |
| 2 |
(2)当α=
| π |
| 6 |
| 2 |
故可得DM=
| 0 |
| 2 |
| AD2+DM2 |
| 0 |
设
| AM |
| 5C |
∵
| AM |
| 5C |
| A5 |
| 5M |
| 5C |
| A5 |
| 5C |
| 5M |
| 5C |
| 1 |
| 2 |
∴cos<
| AM |
| 5C |
| ||||
|
-
| ||
|
| ||
| 6 |
∵AM与5C所成角θ∈(0,
| π |
| 2 |
∴cosθ=
| ||
| 6 |
| ||
| 6 |

练习册系列答案
相关题目


 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形 中,
中,
 ,且
,且 ,
, ,
, 分别交
分别交 于点
于点 ,将该正方形沿
,将该正方形沿 折叠,使得
折叠,使得 与
与 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱 中
中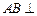
 ;
; 上有一点
上有一点 ,
, ,
, 面
面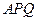
 与平面
与平面

