Question

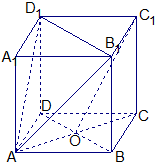
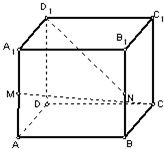
如图，直三棱柱ABC-A₁B₁C₁中，AC=BC=1，AA₁=2，∠ACB=90°，M是A₁B₁的中点．
（1）求证：C₁M⊥平面ABB₁A₁
（2）求异面直线A₁B与B₁C所成角的余弦值．

Answer 1

（1）证明：∵直三棱柱ABC-A₁B₁C₁∴AA₁⊥面A₁B₁C₁
又C₁M?A₁B₁C₁∴C₁M⊥AA₁（2分）∵A₁C₁=B₁C₁=1，M是A₁B₁的中点∴C₁M⊥A₁B₁（4分）
又AA₁∩A₁B₁=A₁∴C₁M⊥平面ABB₁A₁（6分）
（2）设BC，BB₁的中点分别为R、N连接RN，连接MN，则MN∥A₁B，NR∥B₁C
∴∠MNR是异面直线A₁B与B₁C所成角或其补角（9分）
设点P为AB的中点，连接MP，MR
在Rt△MPR中，MR=

22+( 1 2 )2

=
在△MNR中，MN=A₁B=

6

2

，RN=

1

2

B₁C=

5

2

，MR=

17

2

由余弦定理得：
cos∠MNR=

MN2+RN2-MR2

2MN×RN

=

( 6 2 )2+( 5 2 )2-( 17 2 )2

2× 6 2 × 5 2

=-

30

10

（11分）
∴异面直线A₁B与B₁C所成角的余弦值为

30

10

（12分）