题目内容
已知各棱长均为a的正四面体ABCD，E是AD边的中点，连结CE．求CE与底面BCD所成角的正弦值．
作AH⊥底面BCD，垂足H是正△BCD中心，
连DH延长交BC于F，则平面AHD⊥平面BCD，
作EO⊥HD于O，连结EC，
则∠ECO是EC与底面BCD所成的角
则EO⊥底面BCD．
，
∴
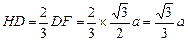
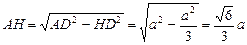
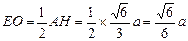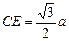
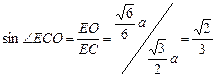
连DH延长交BC于F，则平面AHD⊥平面BCD，
作EO⊥HD于O，连结EC，
则∠ECO是EC与底面BCD所成的角
则EO⊥底面BCD．
，∴
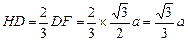
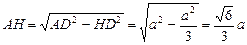
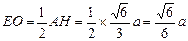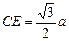
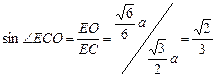
练习册系列答案
相关题目
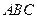
平面
，
，
，△
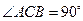的平面角的正切值为多少．
，求: 
平面
，过平面
与
都成
角
的直线有且
AB，点P在平面ABCD上，且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1，在平面直角坐标系xAy中，动点P的轨迹方程是 . 
