题目内容
数列{an}的前n项和为Sn＝2an－2，数列{bn}是首项为a1，公差不为零的等差数列，且b1，b3，b11成等比数列．
(1)求数列{an}与{bn}的通项公式；
(2)求证：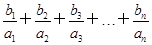
<5.
(1)求数列{an}与{bn}的通项公式；
(2)求证：
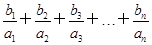<5.（1）bn＝3n－1（2）见解析
(1)当n≥2时，an＝Sn－Sn－1＝(2an－2)－(2an－1－2)＝2an－2an－1，得an＝2an－1.
又由a1＝S1＝2a1－2，得a1＝2，所以数列{an}是以2为首项，2为公比的等比数列，
所以数列{an}的通项公式为an＝2n.
b1＝a1＝2，设公差为d，则由b1，b3，b11成等比数列，得(2＋2d)2＝2×(2＋10d)，
解得d＝0(舍去)或d＝3，
所以数列{bn}的通项公式为bn＝3n－1.，
(2)证明：令Tn＝＝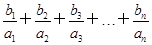
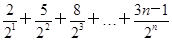，①
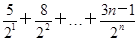2Tn＝2＋
，②
②－①得
Tn＝2＋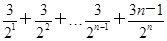
，
所以Tn＝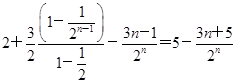
，
又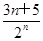
>0，故Tn<5.
又由a1＝S1＝2a1－2，得a1＝2，所以数列{an}是以2为首项，2为公比的等比数列，
所以数列{an}的通项公式为an＝2n.
b1＝a1＝2，设公差为d，则由b1，b3，b11成等比数列，得(2＋2d)2＝2×(2＋10d)，
解得d＝0(舍去)或d＝3，
所以数列{bn}的通项公式为bn＝3n－1.，
(2)证明：令Tn＝
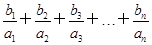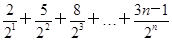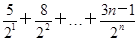＝，①2Tn＝2＋
，②②－①得
Tn＝2＋
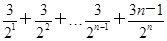，所以Tn＝
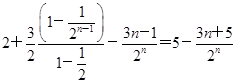，又
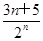>0，故Tn<5.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
,an+1=1-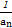
(n≥2),则a16= .
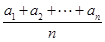也为等差数列．类比这一性质可知，若正项数列{cn}是等比数列，且{dn}也是等比数列，则dn的表达式应为( )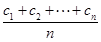
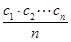
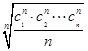
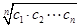
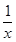(x>0)及两点A1(x1,0)和A2(x2,0)，其中x2>x1>0.过A1，A2分别作x轴的垂线，交曲线C于B1，B2两点，直线B1B2与x轴交于点A3(x3,0)，那么( )
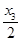，x2成等差数列
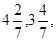…的前n项和为Sn，则使得Sn取得最大值的n的值为（ ）
中，
，则
的值为（ ）