题目内容
若数列{an}是等差数列,则数列{bn}bn=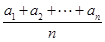 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
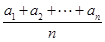 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )A.dn=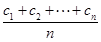 | B.dn=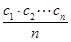 |
C.dn= 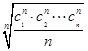 | D.dn=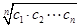 |
D
若{an}是等差数列,
则a1+a2+…+an=na1+ d,
d,
∴bn=a1+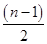 d=
d=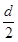 n+a1-
n+a1-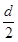 ,
,
即{bn}为等差数列;若{cn}是等比数列,则c1·c2·…·cn=c1n·q1+2+…+(n-1)=c1n·q ,∴dn=
,∴dn=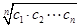 =c1·q
=c1·q ,
,
即{dn}为等比数列,故选D.
则a1+a2+…+an=na1+
 d,
d,∴bn=a1+
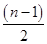 d=
d=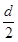 n+a1-
n+a1-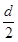 ,
,即{bn}为等差数列;若{cn}是等比数列,则c1·c2·…·cn=c1n·q1+2+…+(n-1)=c1n·q
 ,∴dn=
,∴dn=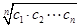 =c1·q
=c1·q ,
,即{dn}为等比数列,故选D.

练习册系列答案
相关题目
 的前
的前 项和为
项和为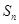 .
.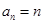 ,数列
,数列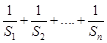 的和.
的和.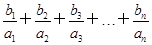 <5.
<5.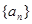 中,
中,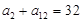 ,则
,则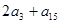 的值是( )
的值是( )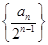 的前n项和.
的前n项和. π,则tan a6=________.
π,则tan a6=________.