题目内容
9.已知集合A={x||x-$\frac{1}{2}$|≤$\frac{3}{2}$},B={x|y=lg(4x-x2)},则A∩B等于( )| A. | (0,2] | B. | [-1,0) | C. | [2,4) | D. | [1,4) |
分析 求出A中不等式的解集确定出A,求出B中x的范围确定出B,找出A与B的交集即可.
解答 解:由A中不等式变形得:-$\frac{3}{2}$≤x-$\frac{1}{2}$≤$\frac{3}{2}$,即-1≤x≤2,即A=[-1,2],
由B中y=lg(4x-x2),得到4x-x2>0,即x(x-4)<0,
解得:0<x<4,即B=(0,4),
则A∩B=(0,2].
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
17.若全集U={x∈R|x2≤4},A={x∈R|-2≤x≤0},则∁UA=( )
| A. | (0,2) | B. | [0,2) | C. | (0,2] | D. | [0,2] |
4.已知函数y=f(x)的定义域是[0,2],那么g(x)=$\frac{f({x}^{2})}{1+lg(x+1)}$的定义域是( )
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
14.已知函数f(x)=|2x-1|,f(a)>f(b)>f(c),则以下情况不可能发生的是( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
1.已知四棱锥P-ABCD的底面四边形ABCD的对边互不平行,现用一平面α去截此四棱锥,且要使截面是平行四边形,则这样的平面α( )
| A. | 有且只有一个 | B. | 有四个 | C. | 有无数个 | D. | 不存在 |
18.过抛物线x2=4y的焦点F作倾斜角为α的直线交抛物线于P、Q两点,过点P作抛物线的切线l交y轴于点T,过点P作切线l的垂线交y轴于点N,则△PNF为( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
19.执行如图所示的程序框图,则输出的S=( )
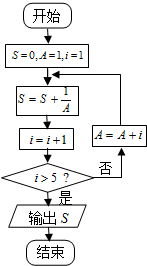

| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |