题目内容
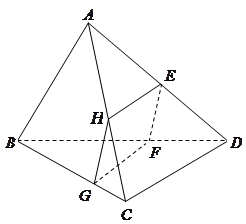
(本题满分10分) 如图,用一付直角三角板拼成一直二面角A—BD—C,若其中给定 AB="AD" =2, ,
, ,
,
(Ⅰ)求三棱锥A-BCD的体积;
(Ⅱ)求点A到BC的距离.
 ,
, ,
, (Ⅰ)求三棱锥A-BCD的体积;
(Ⅱ)求点A到BC的距离.

(Ⅰ)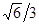 (Ⅱ)
(Ⅱ)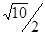
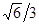 (Ⅱ)
(Ⅱ)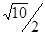
本题考查的知识点是空间点、线、面的距离计算,棱锥的体积,其判断AE⊥平面BCD(即AE是平面BCD上的高)及判断AF垂直BC(即AF长为点A到BC的距离)是解答本题的关键。
(I)由已知中,用一付直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,我们利用面面垂直的性质,我们易求出三棱锥A-BCD的高AE的长,及底面△BCD的面积,代入棱锥体积公式,即可得到答案.
(II)过E点做EF∥CD,利用线面垂直的性质及判定定理,我们易判断AF即为点A到BC的距离,在RT△AEF中,求出AE及EF值后,利用勾股定理,我们易求出AF的值.
(I)由已知中,用一付直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,我们利用面面垂直的性质,我们易求出三棱锥A-BCD的高AE的长,及底面△BCD的面积,代入棱锥体积公式,即可得到答案.
(II)过E点做EF∥CD,利用线面垂直的性质及判定定理,我们易判断AF即为点A到BC的距离,在RT△AEF中,求出AE及EF值后,利用勾股定理,我们易求出AF的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
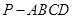 中,底面
中,底面 是矩形,
是矩形, 平面
平面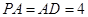 ,
,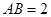 ,点
,点 为
为 的中点,
的中点, 为
为 中点.
中点.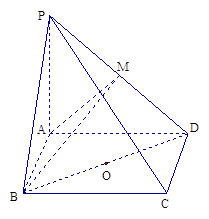
 ⊥平面
⊥平面 ;
;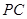 与平面
与平面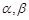 为两个不重合的平面,
为两个不重合的平面,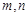 为两条不重合的直线,
为两条不重合的直线,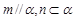 ,则
,则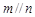 ;
;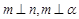 ,则
,则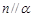 ;
;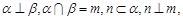 则
则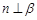 ;
;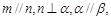 则
则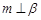 .
. 被一平面所截,截面
被一平面所截,截面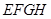 是一个平行四边形.求证:
是一个平行四边形.求证: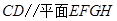 ;
;
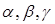 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: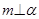 ,
, ,则
,则 ②若
②若 ,
,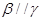 ,
,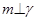
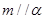 ,
, ④若
④若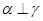 ,
, ,则
,则
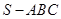 中,各个侧面都是边长为
中,各个侧面都是边长为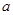 的正三角形,
的正三角形,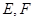 分别是
分别是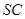 和
和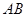 的中点,则异面直线
的中点,则异面直线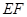 与
与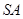 所成的角等于( )
所成的角等于( )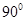
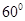
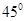
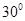
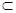 α,则α∥β;
α,则α∥β;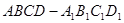 中,
中, 和平面
和平面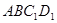 所成的角;
所成的角;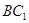 上一点且
上一点且 =
=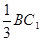 ,在
,在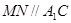 .
.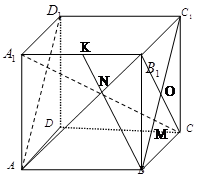
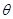 角的直线一定有无穷多条
角的直线一定有无穷多条