题目内容
正方体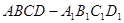 中,
中,
(1)求直线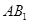 和平面
和平面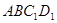 所成的角;
所成的角;
(2)M为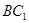 上一点且
上一点且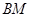 =
=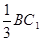 ,在
,在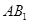 上找一点N使得
上找一点N使得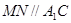 .
.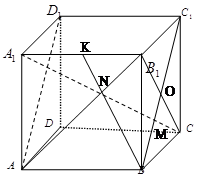
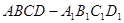 中,
中,(1)求直线
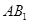 和平面
和平面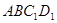 所成的角;
所成的角;(2)M为
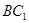 上一点且
上一点且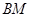 =
=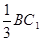 ,在
,在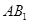 上找一点N使得
上找一点N使得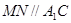 .
.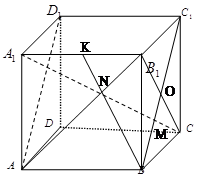
(1)连接

(2)取A1B1中点k,连接OK,则OK//A1C,连接BK交AB1于N,连接MN,则
 …………12分
…………12分

(2)取A1B1中点k,连接OK,则OK//A1C,连接BK交AB1于N,连接MN,则
 …………12分
…………12分略

练习册系列答案
相关题目
题目内容
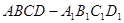 中,
中,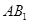 和平面
和平面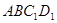 所成的角;
所成的角;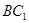 上一点且
上一点且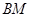 =
=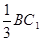 ,在
,在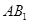 上找一点N使得
上找一点N使得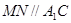 .
.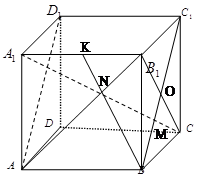

 …………12分
…………12分