题目内容
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:
①若m∥β,n∥β,m、n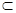 α,则α∥β;
α,则α∥β;
②若α⊥γ,β⊥γ,α∩β=m,n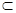 γ,则m⊥n;
γ,则m⊥n;
③若m⊥α,α⊥β,m∥n,则n∥β;
④若n∥α,n∥β,α∩β=m,那么m∥n;
其中所有正确命题的个数是
①若m∥β,n∥β,m、n
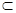 α,则α∥β;
α,则α∥β;②若α⊥γ,β⊥γ,α∩β=m,n
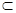 γ,则m⊥n;
γ,则m⊥n;③若m⊥α,α⊥β,m∥n,则n∥β;
④若n∥α,n∥β,α∩β=m,那么m∥n;
其中所有正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
B
解:因为利用线面的位置关系可知,那么
①若m∥β,n∥β,m、n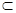 α,则α∥β;错误
α,则α∥β;错误
②若α⊥γ,β⊥γ,α∩β=m,n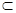 γ,则m⊥n;错误
γ,则m⊥n;错误
③若m⊥α,α⊥β,m∥n,则n∥β; 成立。
④若n∥α,n∥β,α∩β=m,那么m∥n;成立
故选B
①若m∥β,n∥β,m、n
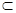 α,则α∥β;错误
α,则α∥β;错误②若α⊥γ,β⊥γ,α∩β=m,n
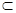 γ,则m⊥n;错误
γ,则m⊥n;错误③若m⊥α,α⊥β,m∥n,则n∥β; 成立。
④若n∥α,n∥β,α∩β=m,那么m∥n;成立
故选B

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
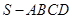 中,底面
中,底面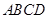 为平行四边形,
为平行四边形,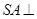 平面
平面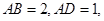
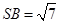
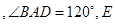 在棱
在棱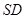 上.
上.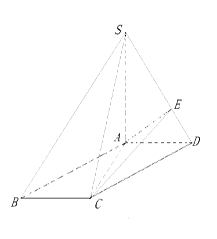
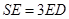 时,求证
时,求证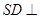 平面
平面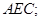
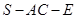 的大小为
的大小为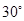 时,求直线
时,求直线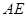 与平面
与平面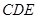 所成角的正弦值.
所成角的正弦值.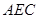 是半径为
是半径为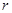 的半圆,
的半圆,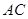 为直径,点
为直径,点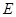 为弧
为弧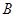 和点
和点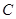 为线段
为线段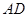 的三等分点,线段
的三等分点,线段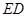 与弧
与弧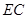 交于点
交于点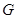 ,且
,且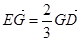 ,平面
,平面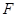 满足
满足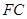
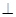 平面
平面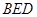 ,
,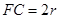 。
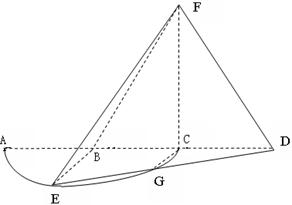
。
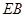
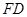 ;
; (及其内部)绕
(及其内部)绕 中,
中,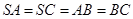 ,则直线
,则直线 与
与 所成角的大小是( )
所成角的大小是( )
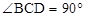 ,
,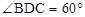 ,
, 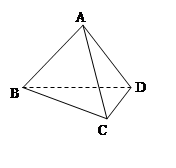
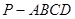 中,
中,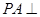 平面
平面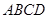 ,
,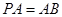
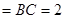 ,
,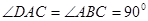 ,
,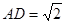 .
.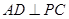 ;
;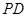 与平面
与平面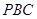 所成角的大小.
所成角的大小.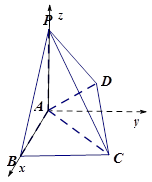
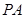 垂直平行四边形
垂直平行四边形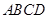 所在平面,若
所在平面,若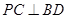 ,则平行则四边形
,则平行则四边形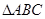 的平面直观图
的平面直观图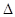 A1B1C1
A1B1C1 是边长为2的正三角形,则原
是边长为2的正三角形,则原