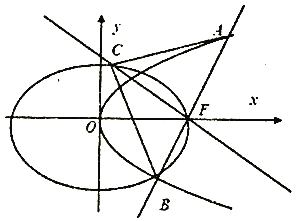
题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 上任意一点,且点
上任意一点,且点![]() 到椭圆
到椭圆![]() 的一个焦点的最大距离等于
的一个焦点的最大距离等于![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同两点
相交于不同两点![]() ,设
,设![]() 为椭圆上一点,是否存在整数
为椭圆上一点,是否存在整数![]() ,使得
,使得![]() (其中
(其中![]() 为坐标原点)?若存在,试求整数
为坐标原点)?若存在,试求整数![]() 的所有取值;若不存在,请说明理由.
的所有取值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)整数
;(Ⅱ)整数![]() 的所有取值为-1,0,1.
的所有取值为-1,0,1.
【解析】试题分析:(Ⅰ)由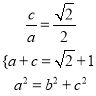 ,解得
,解得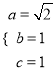 ,则椭圆方程可求;
,则椭圆方程可求;
(Ⅱ)设出直线方程,和椭圆联立后化为关于![]() 的一元二次方程,由判别式大于
的一元二次方程,由判别式大于![]() 求出
求出![]() 的范围,利用根与系数关系得到
的范围,利用根与系数关系得到![]() 两点的横坐标的和与积,代入
两点的横坐标的和与积,代入![]() 后得到
后得到![]() 点的坐标,把
点的坐标,把![]() 点坐标代入椭圆方程后得到
点坐标代入椭圆方程后得到![]() 与
与![]() 的关系,由
的关系,由![]() 的范围确定
的范围确定![]() 的范围.
的范围.
试题解析:(Ⅰ)设椭圆![]() 的半焦距为
的半焦距为![]() ,则由题意知
,则由题意知
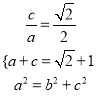 ,解得
,解得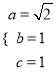 ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)结论:存在整数![]() ,使得
,使得![]() .理由如下:
.理由如下:
由题意知直线![]() 的斜率存在.
的斜率存在.
设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由方程组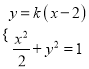 ,消去
,消去![]() 整理得
整理得![]() .
.
∵直线![]() 与椭圆
与椭圆![]() 有两个不同的公共点,
有两个不同的公共点,
∴![]()
![]() ,解得
,解得![]() .
.
而![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴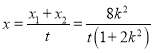 ,
, ![]()
![]()
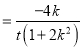 .
.
∵点![]() 在椭圆上,∴
在椭圆上,∴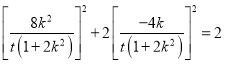 ,
,
∴![]()
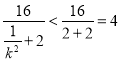 ,即
,即![]() ,解得
,解得![]() ,
,
∴整数![]() 的所有取值为-1,0,1.
的所有取值为-1,0,1.

【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1) 根据题意完成表格;
(2) 是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
参考公式及数据: 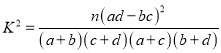 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |