题目内容
1.设(x-$\frac{2}{\sqrt{x}}$)6的展开式中的常数为M,所有二项式系数和为N,则M+N=( )| A. | 304 | B. | -304 | C. | 136 | D. | -136 |
分析 利用(x-$\frac{2}{\sqrt{x}}$)6的展开式中的通项,求出(x-$\frac{2}{\sqrt{x}}$)6的展开式中的常数M,再求出所有二项式系数和N,即可得出结论.
解答 解:(x-$\frac{2}{\sqrt{x}}$)6的展开式中的通项为${T}_{r+1}={C}_{6}^{r}•(-2)^{r}•{x}^{6-\frac{3}{2}r}$,
令6-$\frac{3}{2}$r=0,可得r=4,∴(x-$\frac{2}{\sqrt{x}}$)6的展开式中的常数M=240,
∵所有二项式系数和N=26=64,
∴M+N=240+64=304.
故选:A.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,比较基础.

练习册系列答案
相关题目
6.已知i是虚数单位,则2i(1+i)=( )
| A. | -2+2i | B. | 2+2i | C. | 2i | D. | -2i |
16.在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数.满分100分,按照大于等于80分为优秀,小于80分为合格.为了解学生在该维度的测评结果,从毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表.
下面的临界值表供参考:
已知在该班随机抽取1人测评结果为优秀的概率为$\frac{1}{3}$.
(1)请完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
| 优秀 | 合格 | 总计 | |
| 男生 | 6 | ||
| 女生 | 18 | ||
| 总计 | 60 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)请完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
6.函数f(x)=3x2-x3在下列区间上单调递增的是( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,1) | D. | (0,1) |
13.参数方程$\left\{\begin{array}{l}{x=tanθ}\\{y=\frac{2}{cosθ}}\end{array}\right.$(θ为参数)表示的曲线的离心率( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.与直线l:3x-4y+5=0平行且过点(-1,2)的直线方程为( )
| A. | 4x-3y+10=0 | B. | 4x-3y-11=0 | C. | 3x-4y-11=0 | D. | 3x-4y+11=0 |
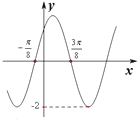 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).