题目内容
4.设函数f(x)=xm+ax的导函数f′(x)=2x+1,则数列{1f(n)}(n∈N*)的前n项和是nn+1.分析 求函数的导数,求出m,a,利用裂项法进行求和.
解答 解:函数的f(x)的导数f′(x)=mxm-1+a,
∵f′(x)=2x+1,
∴m=2,a=1,
即f(x)=x2+x,
则1f(n)=1n2+n=1n(n+1)=1n-1n+1,
则数列{1f(n)}(n∈N*)的前n项和S=1−12+12−13+…+1n-1n+1=1-1n+1=nn+1,
故答案为:nn+1
点评 本题主要考查数列求和,根据导数公式求出函数f(x)的解析式,利用裂项法是解决本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.复数21+i化简的结果为( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
16.在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数.满分100分,按照大于等于80分为优秀,小于80分为合格.为了解学生在该维度的测评结果,从毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表.
下面的临界值表供参考:
已知在该班随机抽取1人测评结果为优秀的概率为\frac{1}{3}.
(1)请完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
| 优秀 | 合格 | 总计 | |
| 男生 | 6 | ||
| 女生 | 18 | ||
| 总计 | 60 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)请完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
13.参数方程\left\{\begin{array}{l}{x=tanθ}\\{y=\frac{2}{cosθ}}\end{array}\right.(θ为参数)表示的曲线的离心率( )
| A. | \frac{\sqrt{3}}{2} | B. | \frac{\sqrt{5}}{2} | C. | \sqrt{2} | D. | 2 |
14.在△ABC中,若a=\sqrt{6},b=2,B={60°},则此三角形( )
| A. | 无解 | B. | 有一解 | ||
| C. | 有两解 | D. | 解的个数无法确定 |
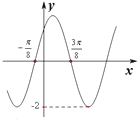 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+