题目内容
3.已知cos(β-$\frac{π}{4}}$)=$\frac{1}{3}$,则sin2β的值等于$-\frac{7}{9}$.分析 由条件和二倍角的余弦公式的变形求出cos2(β-$\frac{π}{4}}$)的值,再利用诱导公式进行化简即可求出sin2β的值.
解答 解:∵cos(β-$\frac{π}{4}}$)=$\frac{1}{3}$,
∴cos2(β-$\frac{π}{4}}$)=2$co{s}^{2}(β-\frac{π}{4})$-1=$-\frac{7}{9}$,
∵cos2(β-$\frac{π}{4}}$)=cos(2β-$\frac{π}{2}$)=sin2β,
∴sin2β=$-\frac{7}{9}$,
故答案为:$-\frac{7}{9}$.
点评 本题考查二倍角的余弦公式的变形,以及诱导公式的灵活应用,解题的关键是能发现角之间的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.复数$\frac{2}{1+i}$化简的结果为( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
6.已知i是虚数单位,则2i(1+i)=( )
| A. | -2+2i | B. | 2+2i | C. | 2i | D. | -2i |
8.在△ABC中,边 a,b,c的对应角分别为A,B,C.若a=1,b=$\sqrt{3},A={30°}$,则B等于( )
| A. | 60° | B. | 60°或120° | C. | 30°或150° | D. | 120° |
13.参数方程$\left\{\begin{array}{l}{x=tanθ}\\{y=\frac{2}{cosθ}}\end{array}\right.$(θ为参数)表示的曲线的离心率( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
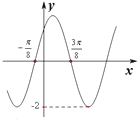 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).