题目内容
2.已知函数f(x)=x2+(a-4)x+3-a(1)若f(x)≤0在区间[0,1]上恒成立,求a的取值范围;
(2)若对于任意的a∈(0,4),存在x1,x2∈[0,2],使得||f(x1)|-|f(x2)||≥t,求t的取值范围.
分析 (1)由题意结合二次函数的性质可得$\left\{\begin{array}{l}{f(0)≤0}\\{f(1)≤0}\end{array}\right.$,解不等式即可得到a的范围;
(2)由题意可得对于任意的a∈(0,4),||f(x)|max-|f(x)|min|≥t由f(1)=0,可得|f(x)|min|=0,
?对于任意的a∈(0,4),|f(x)|max≥t(x∈[0,2]),解法一、讨论对称轴和区间[0,2]的关系,可得最大值和最小值,解法二、运用绝对值不等式的性质,可得|f(x)|的最大值,即可得到t的范围.
解答 解:(1)由题意可得$\left\{\begin{array}{l}{f(0)≤0}\\{f(1)≤0}\end{array}\right.$,
即为$\left\{\begin{array}{l}{3-a≤0}\\{0≤0}\end{array}\right.$,
可得a≥3;
(2)对于任意的a∈(0,4),存在x1,x2∈[0,2],
使得||f(x1)|-|f(x2)||≥t,
?对于任意的a∈(0,4),||f(x)|max-|f(x)|min|≥t
由f(1)=0,可得|f(x)|min|=0,
?对于任意的a∈(0,4),|f(x)|max≥t(x∈[0,2]),
(i)当0<$\frac{4-a}{2}$≤1时,即2≤a<4时,f($\frac{4-a}{2}$)≤f(x)≤f(2)
|f(2)|=|a-1|=a-1,|f($\frac{4-a}{2}$)|=|$\frac{-{a}^{2}+4a-4}{4}$|=$\frac{(a-2)^{2}}{4}$
|f(2)|-|f($\frac{4-a}{2}$)|=$\frac{-{a}^{2}+8a-8}{2}$=$\frac{-(a-4)^{2}+8}{4}$>0,
所以|f(x)|max=a-1;
(ii)当1<$\frac{4-a}{2}$<2时,即0<a<2时,
|f(0)|=|3-a|=3-a,|f($\frac{4-a}{2}$)|=|$\frac{-{a}^{2}+4a-4}{4}$|=$\frac{(a-2)^{2}}{4}$,
|f(0)|-|f($\frac{4-a}{2}$)|=$\frac{8-{a}^{2}}{4}$>0,
|f(x)|max=3-a.
综上,|f(x)|max=$\left\{\begin{array}{l}{a-1,2≤a<4}\\{3-a,0<a<2}\end{array}\right.$
故|f(x)|max≥1,所以t≤1.
解法2:|f(x)|=|(x-1)2+(a-2)(x-1)|
≤(x-1)2+|(a-2)(x-1)|
≤1+|a-2|
等号当且仅当x=0或2时成立,
又(1+|a-2|)min=1,
所以t≤1.
点评 本题考查二次函数的图象和性质的运用,主要考查不等式恒成立问题,注意运用分类讨论和绝对值不等式的性质,考查运算能力,属于中档题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 无解 | B. | 有一解 | ||
| C. | 有两解 | D. | 解的个数无法确定 |
| A. | 4x-3y+10=0 | B. | 4x-3y-11=0 | C. | 3x-4y-11=0 | D. | 3x-4y+11=0 |
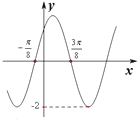 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).