题目内容
【题目】已知数列{an},满足a1=1, ![]() ,n∈N* . (Ⅰ)求证:数列
,n∈N* . (Ⅰ)求证:数列 ![]() 为等差数列;
为等差数列;
(Ⅱ)设 ![]() ,求T2n .
,求T2n .
【答案】证明(Ⅰ):法一:由 ![]() ,得
,得 ![]() =
= ![]() =
= ![]() +
+ ![]() , ∴
, ∴ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴数列{ ![]() }是首项为1,公差为
}是首项为1,公差为 ![]() 的等差数列,
的等差数列,
法二:由 ![]() ,得
,得 ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =(
=( ![]() +
+ ![]() )﹣
)﹣ ![]() =
= ![]()
∴数列{ ![]() }是首项为1,公差为
}是首项为1,公差为 ![]() 的等差数列,
的等差数列,
(Ⅱ)解:设bn= ![]() ﹣
﹣ ![]() =(
=( ![]() ﹣
﹣ ![]() )
) ![]() ,
,
由(Ⅰ)得,数列{ ![]() }是首项为1,公差为
}是首项为1,公差为 ![]() 的等差数列,
的等差数列,
∴ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,
,
即bn=( ![]() ﹣
﹣ ![]() )
) ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() ,
,
∴bn+1﹣bn=﹣ ![]() (
( ![]() ﹣
﹣ ![]() )=﹣
)=﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
且b1=﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() (
( ![]() +
+ ![]() )=﹣
)=﹣ ![]()
∴{bn}是首项b1=﹣ ![]() ,公差为﹣
,公差为﹣ ![]() 的等差数列,
的等差数列,
∴T2n=b1+b2+…+bn=﹣ ![]() n+
n+ ![]() ×(﹣
×(﹣ ![]() )=﹣
)=﹣ ![]() (2n2+3n)
(2n2+3n)
【解析】(Ⅰ)方法一:根据数列的递推公式得到 ![]() =
= ![]() =
= ![]() +
+ ![]() ,即可得到
,即可得到 ![]() ﹣
﹣ ![]() =
= ![]() ,问题得以解决,方法二:根据数列的递推公式得
,问题得以解决,方法二:根据数列的递推公式得 ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =(
=( ![]() +
+ ![]() )﹣
)﹣ ![]() =
= ![]() ,问题得以解决,(Ⅱ)设bn=
,问题得以解决,(Ⅱ)设bn= ![]() ﹣
﹣ ![]() =(
=( ![]() ﹣
﹣ ![]() )
) ![]() ,得到{bn}是首项b1=﹣
,得到{bn}是首项b1=﹣ ![]() ,公差为﹣
,公差为﹣ ![]() 的等差数列,再根据等差数列的求和公式计算即可.
的等差数列,再根据等差数列的求和公式计算即可.
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系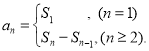 .
.

【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
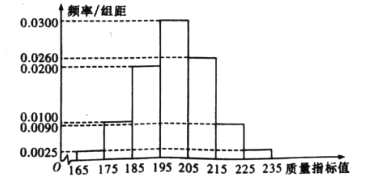
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
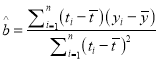 ,
, ![]()