题目内容

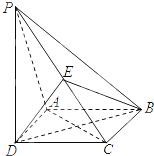
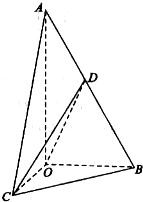
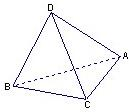
如图，A，B，C，D为空间四点，在△ABC中，AB=2，AC=BC=
2
．等边三角形ADB以AB为轴运动．当CD=______时，面ACD⊥面ADB．
取AB的中点E，连接DE，CE，
因为ADB是等边三角形，所以DE⊥AB．
当平面ADB⊥平面ABC时，
因为平面ADB∩平面ABC=AB，
所以DE⊥平面ABC，
可知DE⊥CE
由已知可得 DE=
3
，EC=1，在Rt△DEC中，CD=
DE2+EC2
=2．
故答案为2
练习册系列答案
相关题目
如图所示，在四棱锥P-ABCD中，底面四边形ABCD是正方形，PD⊥平面ABCD，E为PC的中点．
求证：
（1）PA∥平面BDE；
（2）AC⊥平面PBD．
如图，在长方体ABCD-A1B1C1D1中，底面ABCD是正方形，E是DD1的中点．
（1）求证：AC⊥B1D；
（2）若B1D⊥平面ACE，求
AA1
AB
的值．
如图，已知四棱锥S-ABCD的底面ABCD是矩形，M、N分别是CD、SC的中点，SA⊥底面ABCD，SA=AD=1，AB=
2
．
（I）求证：MN⊥平面ABN；
（II）求二面角A-BN-C的余弦值．
如图，在△ABC中，BD为AC边上的高，BD=1，BC=AD=2，沿BD将△ABD翻折，使得∠ADC=30°，得几何体B-ACD
（Ⅰ）求证：AC⊥平面BCD；
（Ⅱ）求点D到面ABC的距离．
已知一个四棱锥的三视图如图所示，则该四棱锥的四个侧面中，直角三角形的个数是（　　）
A．4B．3C．2D．1
如图，已知三棱锥P-ABC的侧面PAB是等边三角形，D是AB的中点，PC=BC=AC=2，PB=2
2
．
（1）证明：AB⊥平面PCD；
（2）求点C到平面PAB的距离．
已知M是正四面体ABCD棱AB的中点，N是棱CD的中点，则下列结论中，正确的个数有（　　）
（1）MN⊥AB；
（2）VA-MCD=VB-MCD；
（3）平面CDM⊥平面ABN；
（4）CM与AN是相交直线．
A．1个B．2个C．3个D．4个
如图，在三棱锥A-BOC中，AO⊥底面BOC，∠OAB=∠OAC=30°，AB=AC=4，BC=2
2
，动点D在线段AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当点D运动到线段AB的中点时，求二面角D-CO-B的大小；
（Ⅲ）当CD与平面AOB所成角最大时，求三棱锥C-OBD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网