题目内容
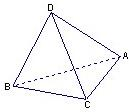
如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得几何体B-ACD
(Ⅰ)求证:AC⊥平面BCD;
(Ⅱ)求点D到面ABC的距离.
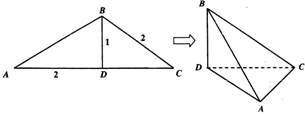
(Ⅰ)求证:AC⊥平面BCD;
(Ⅱ)求点D到面ABC的距离.

(Ⅰ)证明:∵BD⊥AD,BD⊥CD,AD∩CD=D,∴BD⊥平面ACD,
又∵AC?平面ACD,∴AC⊥BD
在△ACD中,∠ADC=
,AD=2,CD=
,
∴AC2=AD2+CD2-2AD•CDcos∠ADC=1
∴AD2=CD2+AC2,∴AC⊥CD,
又BD∩CD=D,∴AC⊥平面BCD.
(Ⅱ)过D点作DE⊥BC,垂足为E点
由(Ⅰ)知:AC⊥平面BCD
∵AC?面ABC
∴面ABC⊥面BCD…(8分)
又∵面ABC∩面BCD=BC
∴DE⊥面ABC
∴DE即为点D到面ABC的距离…(10分)
∵在Rt△BCD中,BC•DE=BD•CD
∴2DE=1×
∴DE=
∴点D到面ABC的距离为
…(12分)
又∵AC?平面ACD,∴AC⊥BD
在△ACD中,∠ADC=
| π |
| 6 |
| 3 |
∴AC2=AD2+CD2-2AD•CDcos∠ADC=1
∴AD2=CD2+AC2,∴AC⊥CD,
又BD∩CD=D,∴AC⊥平面BCD.
(Ⅱ)过D点作DE⊥BC,垂足为E点
由(Ⅰ)知:AC⊥平面BCD

∵AC?面ABC
∴面ABC⊥面BCD…(8分)
又∵面ABC∩面BCD=BC
∴DE⊥面ABC
∴DE即为点D到面ABC的距离…(10分)
∵在Rt△BCD中,BC•DE=BD•CD
∴2DE=1×
| 3 |
∴DE=
| ||
| 2 |
∴点D到面ABC的距离为
| ||
| 2 |

练习册系列答案
相关题目
 底面ABCD,PA=AD=DC=
底面ABCD,PA=AD=DC=