题目内容
5.已知△ABC三边成等差数列,最大角与最小角相差90°,求证:a:b:c=($\sqrt{7}$+1):$\sqrt{7}$:($\sqrt{7}$-1).分析 由题可知,A最大,C最小,则A-C=90°,且2b=a+c,由正弦定理有2sinB=sinA+sinC,利用倍角公式及和差化积公式可得4sin$\frac{B}{2}$cos$\frac{B}{2}$=2sin$\frac{A+C}{2}$cos$\frac{A-C}{2}$=2cos$\frac{B}{2}$cos45°,从而求得sinB进而可求sinA+sinC=$\frac{\sqrt{7}}{2}$,①又由sinA-sinC=2cos$\frac{A+C}{2}$sin$\frac{A-C}{2}$=$\frac{1}{2}$,②,由①,②解得sinA,sinC,从而由正弦定理求得a:b:c=sinA:sinB:sinC的值.
解答 证明:由题可知,A最大,C最小,则A-C=90°,
又∵a、b、c成等差数列,∴有2b=a+c,
由正弦定理有2sinB=sinA+sinC,
即4sin$\frac{B}{2}$cos$\frac{B}{2}$=2sin$\frac{A+C}{2}$cos$\frac{A-C}{2}$=2cos$\frac{B}{2}$cos45°,
∴sin$\frac{B}{2}$=$\frac{\sqrt{2}}{4}$,cos$\frac{B}{2}$=$\frac{\sqrt{14}}{4}$,
∴sinB=$\frac{\sqrt{7}}{4}$,sinA+sinC=2sinB=$\frac{\sqrt{7}}{2}$,①
又∵sinA-sinC=2cos$\frac{A+C}{2}$sin$\frac{A-C}{2}$=2sin$\frac{B}{2}$sin45°=$\frac{1}{2}$,②
由①,②解得sinA=$\frac{\sqrt{7}+1}{4}$,sinC=$\frac{\sqrt{7}-1}{4}$,
由正弦定理,得a:b:c=sinA:sinB:sinC=($\sqrt{7}$+1):$\sqrt{7}$:($\sqrt{7}$-1)
点评 本题主要考查了正弦定理,和差化积公式,倍角公式的应用,考查了等差数列的性质,考查的知识点多,技巧性强,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)>0,f(b)<0 | D. | f(a)<0,f(b)>0 |
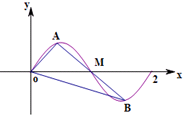 如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )
如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )