题目内容
5.函数y=xsinx+cosx(0<x<2π)的递增区间是(0,$\frac{π}{2}$)和($\frac{3π}{2}$,2π).分析 求导得y'=xcosx,令导函数大于零,求出x的范围
解答 解:y'=xcosx
令xcosx>0
因为x>0
所以cosx>0
所以增区间是(0,$\frac{π}{2}$)和($\frac{3π}{2}$,2π)
故函数的递增区间是(0,$\frac{π}{2}$)和($\frac{3π}{2}$,2π)
点评 考察了符合函数求导和利用导函数判断函数的单调性,是常规题型.

练习册系列答案
相关题目
13.设点M(-1,$\sqrt{3}$)是抛物线y2=2px(p>0)准线上-点,过该抛物线焦点F的直线过A、B两点,若 $\overrightarrow{FM}$•$\overrightarrow{FA}$=0,则△MAB的面积为 ( )
| A. | 2$\sqrt{3}$ | B. | $\frac{5}{2}$$\sqrt{6}$ | C. | 3$\sqrt{6}$ | D. | $\frac{7\sqrt{7}}{2}$ |
10.意义运算“*”如下:x*y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=(1-2x)*(2x-3)+m的图象与x轴有两个交点,则实数m的取值范围是( )
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,+∞) | D. | [-1,1) |
15.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R,若对任意θ∈(0,$\frac{π}{2}$],都有f(msinθ)+f(1-m)>0成立,则实数m的取值范围( )
| A. | (0,1) | B. | (0,2) | C. | (-∞,1) | D. | (-∞,1] |
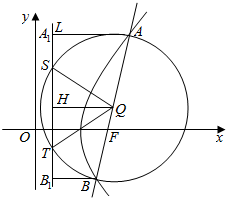 以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:
以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证: