Question

【题目】设为奇函数，为常数．

（1）求证：是上的增函数；

（2）若对于区间上的每一个值，不等式恒成立，求实数取值范围．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）由奇函数的定义域关于原点对称可得，，即，则令，得到的根必为相反数，从而求出a，再根据定义法证明是上的增函数即可；

（2）由题意知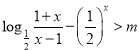，时恒成立，令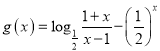，根据单调性的运算可判断的单调性，从而求出最值.

（1）∵是奇函数，∴定义域关于原点对称，

由，得．令，得，，

∴，解得，，令，

设任意，且，则，

∵，∴，，，∴，即．

∴是减函数，又为减函数，

∴在上为增函数；

（2）由题意知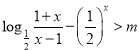，时恒成立，

令，，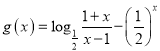

由（2）知在上为增函数，又在上也是增函数，

故在上为增函数，∴的最小值为，

∴，故实数的范围是．