Question

【题目】设M为满足下列条件的函数构成的集合，存在实数，使得.

（1）判断是否为M中的元素，并说明理由；

（2）设，求实数a的取值范围；

（3）已知的图象与的图象交于点，,证明：是中的元素，并求出此时的值（用表示）.

Answer 1

【答案】（1）是；（2）[3﹣，3+]；（3）x0＝，证明见解析

【解析】

根据集合M的定义，可根据函数的解析式f（x0+1）＝f（x0）+f（1）构造方程，若方程有根，说明函数符合集合M的定义，若方程无根，说明函数不符合集合M的定义；

（2）设h（x）＝∈M，则存在实数x，使h（x+1）＝h（x）+h（1）成立，解出a的取值范围即可；

（3）利用f（x0+1）＝f（x0）+f（1）和y＝2ex（x＞）的图象与y＝为图象有交点，即对应方程有根，与求出的值进行比较即可解出x0．

解：（1）设g（x）为M中的元素，则存在实数x0，使得f（x0+1）＝f（x0）+f（1）；

即（x+1）2＝x2+1，∴x＝0，

故g（x）＝x2是M中的元素．

（2）设h（x）＝∈M，则存在实数x，使h（x+1）＝h（x）+h（1）成立；

即lg＝lg+lg；

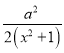∴＝；∴（a﹣2）x2+2ax+2a﹣2＝0，

当a＝2时，x＝﹣；

当a≠2时，则△＝4a2﹣4（a﹣2）（2a﹣2）≥0；

解得a2﹣6a+4≤0，∴3﹣≤a≤3+且a≠2；

∴实数a的取值范围为：[3﹣，3+]．

（3）设m（x）＝ln（3x﹣1）﹣x2∈M，则m（x0+1）＝m（x0）+m（1）；

∴ln[3（x0+1）﹣1]﹣（x0+1）2＝ln（3x0﹣1）﹣x02+ln2﹣1；

∴ln＝2x0；

∴＝；∴＝2；

由于y＝2ex（x＞）的图象与y＝为图象交于点（t，2et），

所以2et＝；

令t＝2x0，则2＝＝；

即存在x0＝，使得则m（x0+1）＝m（x0）+m（1）；

故m（x）＝ln（3x﹣1）﹣x2是M中的元素，此时x0＝．