题目内容
已知双曲线x2-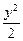 =1,过点A(2,1)的直线l与已知双曲线交于P1、P2两点.
=1,过点A(2,1)的直线l与已知双曲线交于P1、P2两点.
(1)求线段P1P2的中点P的轨迹方程;
(2)过点B(1,1)能否作直线l′,使l′与已知双曲线交于两点Q1、Q2,且B是线段Q1Q2的中点?请说明理由.
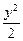 =1,过点A(2,1)的直线l与已知双曲线交于P1、P2两点.
=1,过点A(2,1)的直线l与已知双曲线交于P1、P2两点.(1)求线段P1P2的中点P的轨迹方程;
(2)过点B(1,1)能否作直线l′,使l′与已知双曲线交于两点Q1、Q2,且B是线段Q1Q2的中点?请说明理由.
(1) 中点P的轨迹方程是2x2-y2-4x+y=0. (2)见解析
(2)见解析
 (2)见解析
(2)见解析(1)解法一:设点P1、P2的坐标分别为(x1,y1)、(x2,y2),中点P的坐标为(x,y),则有x12-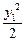 =1,x22-
=1,x22-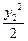 =1,两式相减,得
=1,两式相减,得
2(x1+x2)(x1-x2)=(y1+y2)(y1-y2).
当x1≠x2,y≠0时,
由x1+x2=2x,y1+y2=2y,
得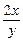 =
= . ①
. ①
又由P1、P2、P、A四点共线,
得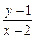 =
= . ②
. ②
由①②得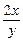 =
=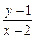 ,
,
即2x2-y2-4x+y=0.
当x1=x2时,x=2,y=0满足此方程,故中点P的轨迹方程是2x2-y2-4x+y=0.
解法二:设点P1、P2、中点P的坐标分别为(x1,y1)、(x2,y2)、(x,y),
直线l的方程为y=k(x-2)+1,将l方程代入双曲线x2-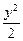 =1中,
=1中,
得(2-k2)x2+2k(2k-1)x+2k2-3=0,
则x1+x2=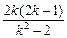 ,x1x2=
,x1x2=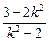 ,
,
y1+y2=k(x1+x2)+2-4k=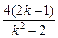 .
.
 于是
于是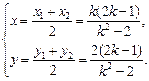
当y≠0时,由①②得k=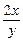 .将其代入①,整理得2x2-y2-4x+y=0.当l倾斜角为90°时,P点坐标为(2,0)仍满足此方程,故中点P的轨迹方程为2x2-y2-4x+y=0.
.将其代入①,整理得2x2-y2-4x+y=0.当l倾斜角为90°时,P点坐标为(2,0)仍满足此方程,故中点P的轨迹方程为2x2-y2-4x+y=0.
(2)假设满足题设条件的直线l′存在,Q1、Q2的坐标分别为(x3,y3)、(x4,y4),同(1)得2(x3+x4)(x3-x4)=(y3+y4)(y3-y4).
∵x3+x4=2,y3+y4=2,
∴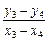 =2(x3≠x4),
=2(x3≠x4),
即l′的斜率为2.
∴l′的直线方程为y-1=2(x-1),
即y=2x-1.
∵方程组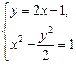 无解,与假设矛盾,
无解,与假设矛盾,
∴满足条件的直线l′不存在.
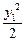 =1,x22-
=1,x22-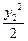 =1,两式相减,得
=1,两式相减,得2(x1+x2)(x1-x2)=(y1+y2)(y1-y2).
当x1≠x2,y≠0时,
由x1+x2=2x,y1+y2=2y,
得
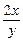 =
= . ①
. ①又由P1、P2、P、A四点共线,
得
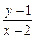 =
= . ②
. ②由①②得
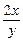 =
=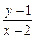 ,
,即2x2-y2-4x+y=0.
当x1=x2时,x=2,y=0满足此方程,故中点P的轨迹方程是2x2-y2-4x+y=0.
解法二:设点P1、P2、中点P的坐标分别为(x1,y1)、(x2,y2)、(x,y),
直线l的方程为y=k(x-2)+1,将l方程代入双曲线x2-
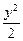 =1中,
=1中,得(2-k2)x2+2k(2k-1)x+2k2-3=0,
则x1+x2=
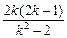 ,x1x2=
,x1x2=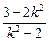 ,
,y1+y2=k(x1+x2)+2-4k=
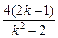 .
. 于是
于是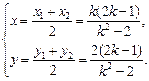
当y≠0时,由①②得k=
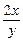 .将其代入①,整理得2x2-y2-4x+y=0.当l倾斜角为90°时,P点坐标为(2,0)仍满足此方程,故中点P的轨迹方程为2x2-y2-4x+y=0.
.将其代入①,整理得2x2-y2-4x+y=0.当l倾斜角为90°时,P点坐标为(2,0)仍满足此方程,故中点P的轨迹方程为2x2-y2-4x+y=0.(2)假设满足题设条件的直线l′存在,Q1、Q2的坐标分别为(x3,y3)、(x4,y4),同(1)得2(x3+x4)(x3-x4)=(y3+y4)(y3-y4).
∵x3+x4=2,y3+y4=2,
∴
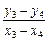 =2(x3≠x4),
=2(x3≠x4),即l′的斜率为2.
∴l′的直线方程为y-1=2(x-1),
即y=2x-1.
∵方程组
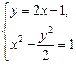 无解,与假设矛盾,
无解,与假设矛盾,∴满足条件的直线l′不存在.

练习册系列答案
相关题目
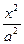 -
- =1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于___________.
=1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于___________.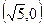 和曲线
和曲线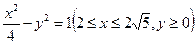 上的点
上的点 …、
…、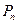 。若
。若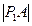 、
、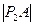 、…、
、…、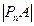 成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若
成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若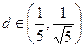 ,是否存在满足条件的
,是否存在满足条件的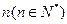 .若存在,求出n可取的所有值,若不存在,说明理由.
.若存在,求出n可取的所有值,若不存在,说明理由.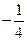
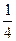
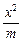 +
+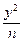 =1(m>n>0)和双曲线
=1(m>n>0)和双曲线 -
-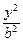 =1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
=1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是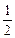 (m-a)
(m-a)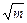 -
-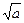
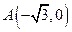 和
和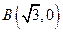 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线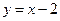 交于D、E两点,求线段DE的长.
交于D、E两点,求线段DE的长.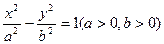 的右顶点为E,双曲线的左准线与该双曲线的两渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率e是()
的右顶点为E,双曲线的左准线与该双曲线的两渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率e是()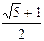
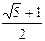 或2
或2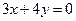 ,一焦点为(4,0)的双曲线标准方程是
,一焦点为(4,0)的双曲线标准方程是 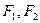 是双曲线
是双曲线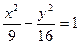 的两个焦点,点P在双曲线上且满足
的两个焦点,点P在双曲线上且满足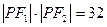 ,
,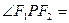 ————
————