题目内容
20.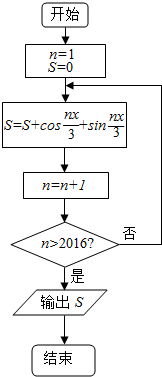 如图所示程序框图中,输出S=( )
如图所示程序框图中,输出S=( )| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{3}$ |
分析 模拟执行程序框图,依次写出每次循环得到的n,S的值,当n=2017时,满足条件n>2016,退出循环,输出S的值,利用正弦函数,余弦函数的取值的周期性即可求值.
解答 解:模拟执行程序框图,可得
n=1,S=0,
S=cos$\frac{π}{3}$+sin$\frac{π}{3}$,
n=2,不满足条件n>2016,S=(cos$\frac{π}{3}$+sin$\frac{π}{3}$)+(cos(2×$\frac{π}{3}$)+sin(2×$\frac{π}{3}$)),
…
n=2016,不满足条件n>2016,S=(cos$\frac{π}{3}$+sin$\frac{π}{3}$)+(cos(2×$\frac{π}{3}$)+sin(2×$\frac{π}{3}$))+…+(cos(2016×$\frac{π}{3}$)+sin(2016×$\frac{π}{3}$)),
n=2017,满足条件n>2016,退出循环,输出S=(cos$\frac{π}{3}$+sin$\frac{π}{3}$)+(cos(2×$\frac{π}{3}$)+sin(2×$\frac{π}{3}$))+…+(cos(2016×$\frac{π}{3}$)+sin(2016×$\frac{π}{3}$))的值.
∵sin$\frac{kπ}{3}$+sin$\frac{(k+1)π}{3}$+sin$\frac{(k+2)π}{3}$+sin$\frac{(k+3)π}{3}$+sin$\frac{(k+4)π}{3}$+sin$\frac{(k+5)π}{3}$=0,k∈Z,且cos$\frac{kπ}{3}$+cos$\frac{(k+1)π}{3}$+cos$\frac{(k+2)π}{3}$+cos$\frac{(k+3)π}{3}$+cos$\frac{(k+4)π}{3}$+cos$\frac{(k+5)π}{3}$=0,k∈Z,2016=6×336,
∴可得:S=0.
故选:B.
点评 本题主要考查了循环结构的程序框图,考查了正弦函数,余弦函数的取值的周期性,属于基本知识的考查.

(1)当x>1时,方程f(x)=0有解,求a的取值范;
(2)若存在x0∈R,使得f(x0)<0与g(x0)<0同时成立,求a的取值范围.
| A. | y=-x2 | B. | y=x-1 | C. | y=log2|x| | D. | y=-2x |
| A. | $({\frac{1}{4},+∞})$ | B. | (0,$\frac{1}{4}$) | C. | $({-∞,\frac{1}{4}})$ | D. | $({-∞,\frac{1}{4}})∪({\frac{1}{4},+∞})$ |